An improved method of computing a discrete approximation of the Laplacian of a Gaussian convolution of an image has been devised. The primary advantage of the method is that without substantially degrading the accuracy of the end result, it reduces the amount of information that must be processed and thus reduces the amount of circuitry needed to perform the Laplacian-of-Gaussian (LOG) operation.
Some background information is necessary to place the method in context. The method is intended for application to the LOG part of a process of real-time digital filtering of digitized video data that represent brightnesses in pixels in a square array. The particular filtering process of interest is one that converts pixel brightnesses to binary form, thereby reducing the amount of information that must be performed in subsequent corre-lation processing (e.g., correlations between images in a stereoscopic pair for determining distances or correlations between successive frames of the same image for detecting motions). The Laplacian is often included in the filtering process because it emphasizes edges and textures, while the Gaussian is often included because it smooths out noise that might not be consistent between left and right images or between successive frames of the same image.
For the purpose of processing digitized image data, the Gaussian and Laplacian values of a pixel of interest are approximated as weighted sums of brightnesses of the pixels in a square subarray (typically 3 x 3) of pixels centered on the pixel of interest. The weights are represented by coefficient matrices, the elements of which correspond to pixels in the subarray. For example,
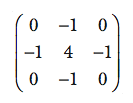
gives a reasonable approximation of the Laplacian for a 3 ´ 3 subarray.
A typical prior state-of-the-art LOG algorithm operates in a sequential raster-oriented pixel stream, and the kernel is factored as much as possible into 1 × 3 and 3 × 1 components. To apply a 1 × 3 or a 3 × 3 kernel to the pixel in a given row and column, it is necessary to retain the pixel stream in two raster-length delay lines so that the pixels in the adjacent rows and columns remain available for the computation. Heretofore, 12 bits of precision have been needed to maintain accuracy sufficient for reasonable convolution results through several stages. Usually, the Laplacian operation is performed first to normalize the image data about 0. This concludes the background information.
In the present method, intermediate results are approximated in such a way that only 6 or possibly even as few as four bits are retained, yet the final result is still reasonable. If only 6 bits of precision are needed rather than 12, the size of the memory circuitry needed to implement the delay lines can be halved. Thus, it should be possible to build smaller, lower-power filtering circuits.

Heretofore, it has been common practice in limited-precision arithmetic circuitry to approximate large values by truncating them, eliminating the least significant bits. However, a detailed analysis of the arithmetic process shows that eliminating the bits of lowest order can lead to errors in the final conversion to binary representation. In the present method, the least significant bits are retained and large values are approximated by a saturation technique based on the unconventional approach of discarding the highest-order bits. If the magnitude of a pixel value is larger than the largest magnitude that can be represented in the result, then the pixel value is replaced by a value of the same sign (positive or negative) and the largest representable magnitude.
The figure depicts an example of a circuit that utilizes 2's-complement encoding of negative numbers and that implements saturation of a six-bit quantity to a four-bit quantity. The exclusive-OR gates examine the number of high-order bits to be eliminated, plus one, to determine whether they are already all alike. If the examined input bits are not all alike, a maximum positive or negative quantity is derived from the sign bit and gated through the multiplexer. This is easily extended to handle a reduction of any number of bits.
This work was done by Robert L. Shuler, Jr., of Johnson Space Center. MSC-22954.

