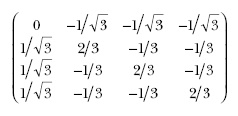A quantum algorithm provides for the encoding of an exponentially large number of classical data bits by use of a smaller (polynomially large) number of quantum bits (qubits). The development of this algorithm was prompted by the need, heretofore not satisfied, for a means of entering real-world binary data into a quantum computer. The data format provided by this algorithm is suitable for subsequent ultrafast quantum processing of the entered data. Potential applications lie in disciplines (e.g., genomics) in which one needs to search for matches between parts of very long sequences of data. For example, the algorithm could be used to encode the N-bit-long human genome in only log2N qubits. The resulting log2N-qubit state could then be used for subsequent quantum data processing — for example, to perform rapid comparisons of sequences.

Below are the steps of the algorithm, illustrated with the example of the fourbit string 0111:

  1. Specify a correspondence between (a) each classical bit in a string of 2n such bits and (b) a unique n-bit eigenstate in a set of 2n such eigenstates. For example, if a classical 2n-bit string is 0111, then the corresponding four 2-bit eigenstates could be |00>, |01>, |10>, and |11>.
  2. Construct a superposition, |ψ>, of equally weighted quantum states that is peaked at only those eigenstates that correspond to 1s in the classical bit string. In the example of the bit string 0111, the corresponding 2-qubit state would be |ψ>= 3-1/2 (|01> + |10> + |11>). In the general case, the superposition would be an entangled state of n qubits that encodes a specific sequence of 2n classical bits.

  3. Compute the unitary transformation needed to obtain the superposition starting from an easy-to-make state (for example, |00>). Equivalently, compute a unitary matrix that maps the chosen state (e.g., |00>) into the state |ψ>. For the classical bit string 0111, the unitary matrix would be

    To compute the matrix, first compute |ψ><ψ| (which gives one column of the matrix), then generate the remaining orthonormal vectors for the other columns.

  4. By use of software developed previously for this purpose, compute the form of a feasible quantum circuit equivalent to the unitary matrix. The quantum circuit could be implemented in one of several physical embodiments: for example, spin-based, charge-based, optical, or superconducting quantum computer hardware.

This work was done by Colin Williams of Caltech for NASA’s Jet Propulsion Laboratory. For further information, access the Technical Support Package (TSP) free on-line at www.techbriefs.com/tsp under the Information Sciences category.

In accordance with Public Law 96-517, the contractor has elected to retain title to this invention. Inquiries concerning rights for its commercial use should be addressed to:

Innovative Technology Assets Management
JPL
Mail Stop 202-233
4800 Oak Grove Drive
Pasadena, CA 91109-8099
(818) 354-2240
E-mail: This email address is being protected from spambots. You need JavaScript enabled to view it.

Refer to NPO-30209, volume and number of this NASA Tech Briefs issue, and the page number.

Topics:
Computer software and hardware Information Technology Logistics Mathematical models Optics Simulation and modeling
This Brief includes a Technical Support Package (TSP).
Document cover
Scheme for Entering Binary Data Into a Quantum Computer

(reference NPO-30209) is currently available for download from the TSP library.

Don't have an account?

Magazine cover
NASA Tech Briefs Magazine

This article first appeared in the March, 2005 issue of NASA Tech Briefs Magazine (Vol. 29 No. 3).

Read more articles from the archives here.

Overview

The document is a Technical Support Package from NASA's Jet Propulsion Laboratory (JPL) detailing a novel scheme for encoding classical binary data into quantum computers. This innovative approach allows for the exponential compression of classical data into a quantum state, enabling efficient quantum data processing. The method is structured into four key steps:

  1. Bit String-Eigenstate Correspondence: The process begins by establishing a one-to-one correspondence between a string of classical bits and n-bit eigenstates. For instance, a bit string like "0111" corresponds to specific eigenstates.

  2. Mapping Bits to Superposition State: The next step involves constructing an equally weighted superposition of quantum states that correspond to the "1" bits in the classical string. This results in an entangled state of quantum bits (qubits) that encodes the classical information.

  3. Unitary Transformation Computation: A unitary transformation is computed to convert a simple initial state into the desired superposition state. This transformation is essential for encoding the classical data into the quantum format.

  4. Quantum Circuit Implementation: Finally, the unitary transformation is translated into a quantum circuit using a specialized software tool. This circuit design is crucial for implementing the encoding process in a physical quantum computing environment.

The software developed as part of this project is notable for its ability to encode an exponential number of classical bits using only a polynomial number of qubits, which represents a significant advancement in quantum computing. The potential applications of this technology are vast, including fields such as genomics, surveillance, remote sensing, and financial markets.

The document also highlights the contributions of JPL personnel involved in the project and discusses the commercial potential of the software, particularly for companies engaged in quantum computing hardware development, such as D-Wave Systems.

Overall, this Technical Support Package outlines a significant step forward in the integration of classical data with quantum computing, paving the way for more efficient data processing and broader applications in various industries. The work is positioned as a foundational advancement that could enhance the capabilities of quantum computers in handling real-world data challenges.