Alens is cylindrical. It captures light in a circular plane for collection onto a rectangular digital sensor plane. This collection of photons is then transformed into electricity by smaller square pixels. Just how do these disparate shapes work together to provide usable images?
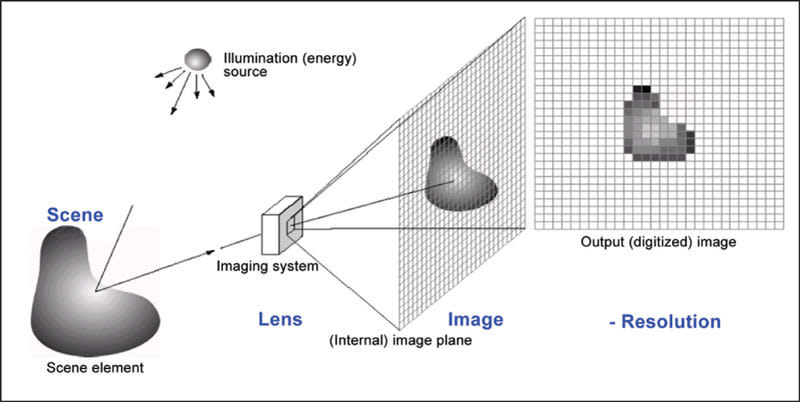
A digital imaging system consists of a light collector (lens), a light receptor (sensor) and light transformers (pixels). The object of digital imaging is to transform the light from the surroundings into electronic information analogous to those surroundings. For a machine vision system, the light from an object in the surroundings is selected for exclusive analysis and the electronic information is transformed into data so that a machine can make a decision (Where is object, what color, how many holes, etc.?).
Figure 1 illustrates the digital imaging process. Photons are provided by an illumination source such as a controlled light source or the sun. These photons impact a scene or object, whereupon some are absorbed and some are reflected. The wavelength (remember that light behaves as waves and particles) of the reflected light determines its color while the surface determines the amount of light and at what angle the light is reflected. Photons from the scene become available to the lens from a variety of angles and directions. These light waves pass through one or more stages of the lens, where they are bent, or refracted, per the lens design to be projected onto the focal plane of the media, which for our discussion is a digital image sensor. This sensor is a matrix of smaller (usually) square picture elements (pixels) that convert the photons into electrons for further transformation downstream by software into usable image information.
A Round Lens
A lens consists of a cylinder into which one or more disks of glass have been inserted. The disks have been ground to achieve certain desired refractive effects. Light emanating from an illumination source reflects off a scene or object. The angles of reflection are always equal to the angle at which the light was sourced, but light at different angles reaches the lens based on the composition and geometry of the object.
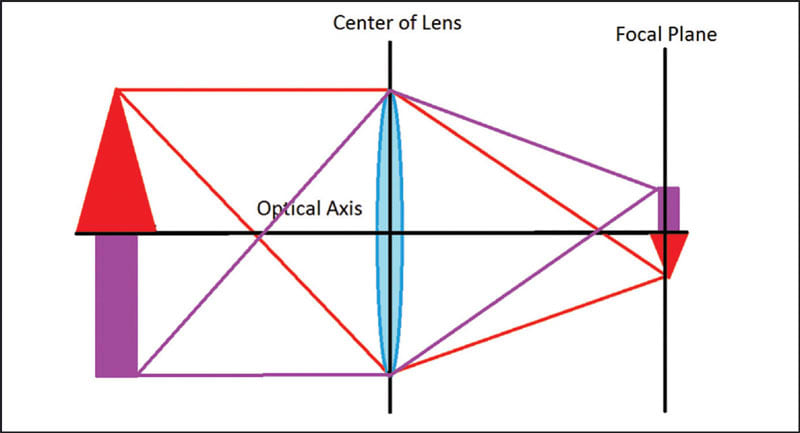
Figure 2 is a side view illustrating a simple lens, the originating object, and the resulting image. Note that the image is inverted from the object and that all the light from the object is refracted by the entire lens, albeit at different angles. Note also that the light that enters closest to the optical axis is refracted less and is thus less distorted. In other words, the portion of the image at the center of the lens is more accurate than that at the periphery. This has many implications discussed elsewhere regarding f-number, depth of field and optical aberrations.
Figure 3 illustrates the image circle resulting from the projection of light through the cylinder disks onto the sensor. The image is inverted and light from the entire object is present. If we were to occlude the lens partially, we would observe that the image wouldremain inverted and the entire object would remain visible, although less bright and perhaps out of focus where the occlusion occurred. Note also that the resultant projection onto the media is a circle. This “image circle” is important as it relates to the rectangular media (image sensor).
Rectangular Sensor
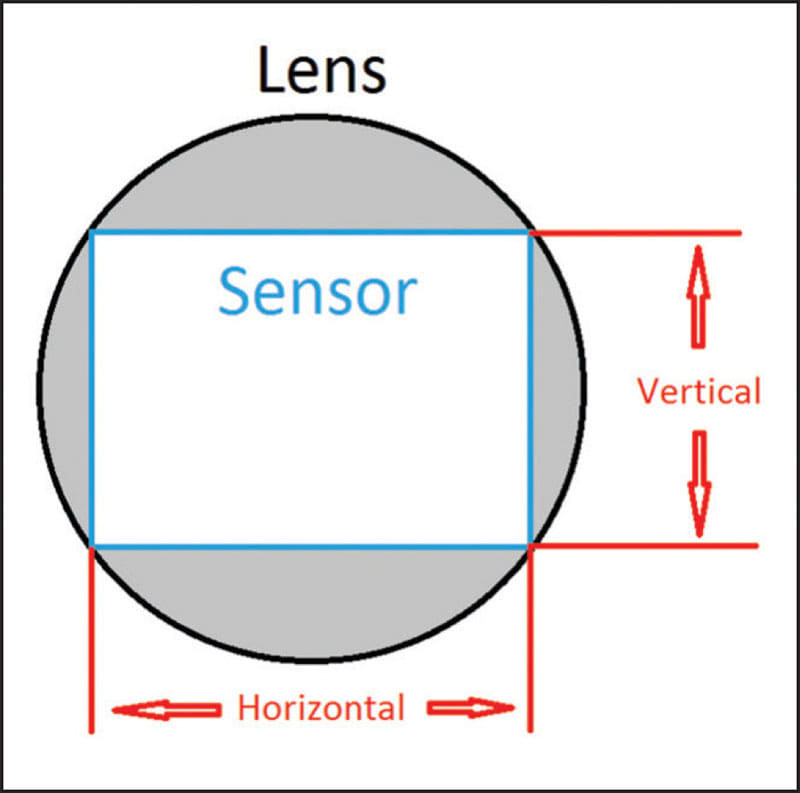
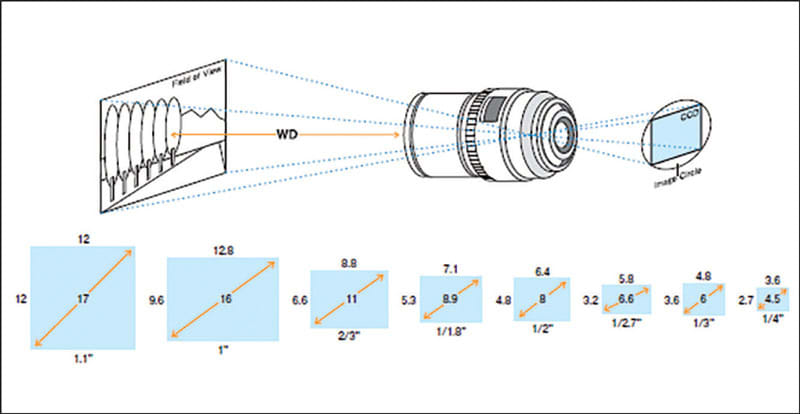
The lens creates a circular image, but the sensor is rectangular. To understand the relationship between the two, it is valuable to know the aspect ratio of the sensor (Figure 4).
Aspect ratio refers to the ratio between the horizontal and the vertical axes of the sensor. It is commonly expressed as two numbers separated by a colon (e.g. 1:1, 4:3, etc.). As a rule, aspect ratios closest to 1:1 yield greater image accuracy.
While the aspect ratio describes the sensor geometry, the sensor format describes its size. (Figure 5). Sensor format is the diagonal distance resulting from a pixel matrix with a given aspect ratio. It describes the minimum diameter of the image circle of the lens to maximize the area of the sensor. Lenses are specified according to the sensor size (format) they will support without vignetting.
Larger image circles will support equal or smaller sensor sizes. For example, a 2/3” lens may be used with a 2/3” camera sensor or with a ½” sensor without vignetting.
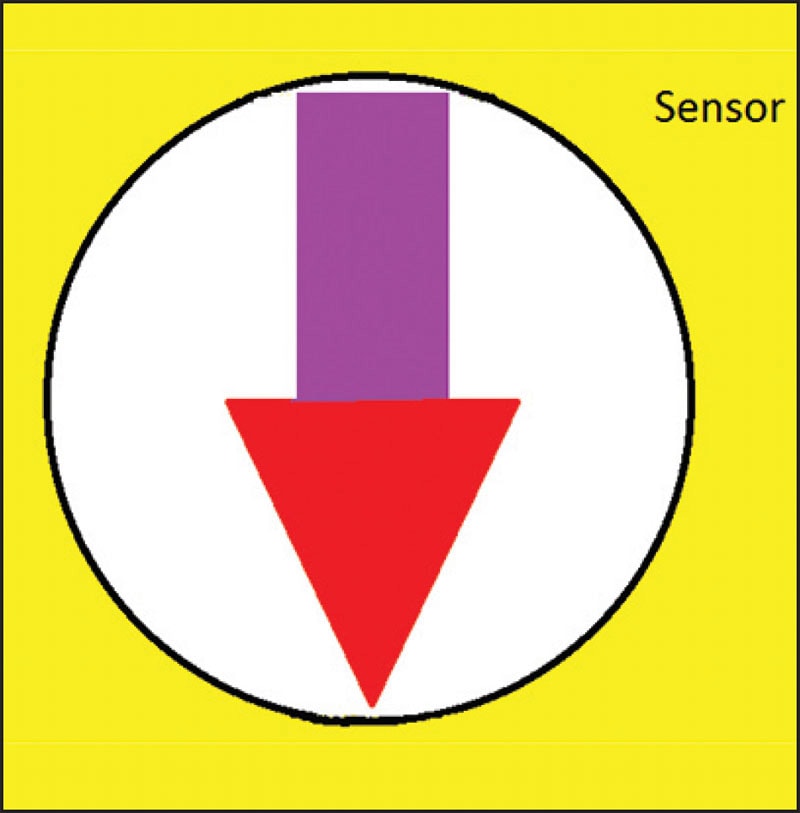
Vignetting (Figure 6) (Wikipedia, Vignetting, 2016) is an optical aberration where the rectangular media (sensor) is only partially illuminated by the circular projected image from the lens. As pointed out in the previous section, the optical distortion is less at the center of the lens than at the periphery. Thus, at times a vision system designer may wish to sacrifice Field of View in favor of aberration control, improving contrast and sharpness (Walree, 2002-2016).
Square Pixels


Figure 7 illustrates an image projected upon a pixel matrix. Although exaggerated, the principles illustrated are valid. Note the diminishing and irregular lighting at the periphery of the image window. Note, too, the pixel geometry manifested in the image. That is, between every pair of pixels, there is a finite border at which light is not detected. Also, to determine the location of the curve or diagonal color change, two pixels are required. In the case of the head of the arrow, to know where the edge of the arrow is one must detect both a white and a red pixel, and probably even a pink one that’s a little of both colors along the diagonal.
The degree of detail that can be detected is a matter of the size and number of pixels in the matrix: more and smaller pixels allow the detection of finer detail. Smartphones and DSR cameras have software that compensates for resolution and lens aberrations, and square pixels help simplify these calculations. This software makes assumptions about a pixel and its neighbors and adjusts the image output to make the image more pleasing to the human eye. In machine vision applications, however, such software introduces a high degree of noise into the process. Machine vision algorithms also make assumptions about pixel values, but they do so from a raw video signal and with the intent to replicate the actual image. Resolution and pixel size of the sensor are still important, as are the format and quality of the lens.
The benefits of a high-resolution sensor are not realized without a high-resolution lens. Lens resolution is specified in line-pairs per millimeter (lp/mm). This value is known as the spatial frequency, and just as two pixels allow the detection of an edge, so a line pair also allows the detection of an edge. The terms “optical transfer function” (OTF) or “modulus transfer function” (MTF) are used to specify the degree of contrast between two lines as transmitted by the lens. Unlike the sensor pixel matrix, OTF can vary across the diameter of the lens, so specialized charts are used to describe this feature.
Conclusion
Between the round lens and the square pixels, there is refraction, projection, and interpretation. Yet, millions of complex, automated measurements and flaw detection operations are performed daily. It’s simply a matter of applying the laws of physics.
This article was written by Pete Kepf, CVP-A, Lens Business Development Executive, CBC AMERICAS Corp., Industrial Optics Division (Cary, NC). For more information, contact Mr. Kepf at

