
Combustion instability in solid rocket motors and liquid engines is a complication that continues to plague designers and engineers. Many rocket systems experience violent fluctuations in pressure, velocity, and temperature originating from the complex interactions between the combustion process and gas dynamics. During severe cases of combustion instability, fluctuation amplitudes can reach values equal to or greater than the average chamber pressure. Large amplitude oscillations lead to damaged injectors, loss of rocket performance, damaged payloads, and, in some cases, breach of case/loss of mission. Historic difficulties in modeling and predicting combustion instability haves reduced most instances of most rocket systems experiencing instability into a costly fix through testing or scrapping of the system entirely.
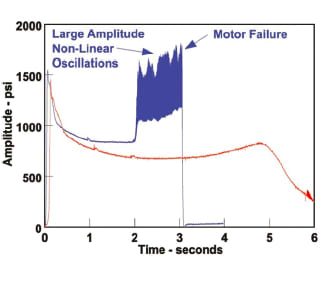
During the early development of rocket propulsion technology, scientists and engineers were cued to the underlying physics at play through the measurement of vibrating test stands, observation of fluctuating exhaust plumes, and most notably, the audible tones accompanying instabilities. These observations lead the pioneers of combustion instability research to acutely focus their modeling efforts on the acoustic waves inside combustion chambers. This focus on acoustics is quite logical given that the measured frequency of oscillation often closely matches the normal acoustic modes of the combustion chamber. But this narrow focus misses contributions made by rotational and thermal waves that are a direct result of, or closely couple with, the acoustic wave. A more complete depiction of combustion instability oscillations is achieved when a global energy-based assessment is used.
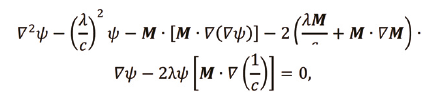
Recent advances in energy-based modeling of combustion instabilities require an accurate determination of acoustic frequencies and mode shapes. Of particular interest are the acoustic mean flow interactions within the converging section of a rocket nozzle, where gradients of pressure, density, and velocity become large. The expulsion of unsteady energy through the nozzle of a rocket is identified as the predominant source of acoustic damping for most rocket systems. Recently, an approach to address nozzle damping with mean flow effects was implemented by French2. This new approach extends the work originated by Sigman and Zinn3 by solving the acoustic velocity potential equation (AVPE) formulated by perturbing the Euler equations4.
Determining eigenvalues of the AVPE, Figure 3 is considerably more complex than the traditionally used pressure based wave equation, Figure 4, and requires numerical approximations of the chamber flow-field and eigenvalues.
Modeling Chamber Gas Dynamics
The latest theoretical models for oscillatory disturbances in high-speed flows require a precise determination of the chamber acoustic eigenmodes. But first, a simulation of the mean flow properties of the combustion chamber must be performed. COMSOL Multiphysics provides a numerical platform for conveniently and accurately simulating both the chamber gas dynamics and internal acoustics. This finite element software package provides multiple predefined physics modules along with a generalized mathematics module.
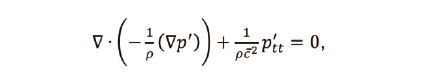
The present study employs the COMSOL Multiphysics finite element framework to model the steady flow-field parameters of a generic liquid engine using the laminar flow equations within the software’s High Mach Number Flow (HMNF) physics module. The HMNF module makes use of these fully compressible Navier-Stokes equations for an ideal gas, which are detailed in the COMSOL documentation.
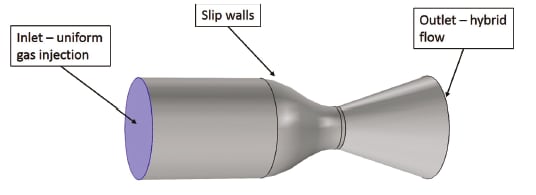
In order to account for the injection of hot gas due to the burning propellant, the injector face plate is modeled with a uniform inward flow of combusted propellant gas. All other solid boundaries are modeled with the slip boundary condition, and the exit plane is modeled with the hybrid outflow condition.
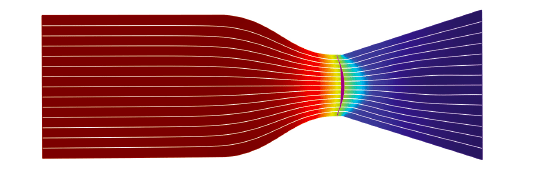
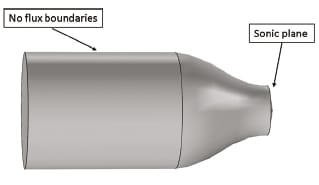
Results from the HMNF analysis are reviewed to assure a valid and converged solution. Mean flow parameters such as pressure, density, velocity, and speed of sound are needed to model the AVPE. Of considerable interest are the values of the mean flow in the converging section of the nozzle, near the sonic choke plane. The sonic plane, where Mach number is equal to one, creates an acoustic barrier in the flow. In order to create an accurate geometry for the acoustic analysis, the sonic plane (pictured in magenta in Figure 6) is extracted from the HMNF analysis.
Modeling Chamber Acoustics
The Coefficient Form Partial Differential Equation module of COMSOL Multiphysics is used to determine the complex eigenvalues of the AVPE. Mean flow terms in the AVPE are supplied by the solution from the HMNF analysis. Gas dynamics within the combustion chamber play a key role in defining the boundary conditions for the acoustic analysis. Within the converging and diverging section of the rocket nozzle, gradients of chamber pressure, velocity, and density grow theoretically infinite at the sonic (Mach number equal to 1) plane. Downstream of the sonic plane, acoustic disturbances are convected with the mean flow at speeds greater than the speed of sound. This condition prevents disturbances downstream of the sonic plane from propagating back upstream. The diverging section of the nozzle is acoustically silent, and does not affect the chamber acoustics. The simulation geometry is truncated at the nozzle sonic line, where a zero flux boundary condition is self-satisfying. The remaining boundaries are modeled with a zero flux boundary condition, assuming zero acoustic absorption on all surfaces.
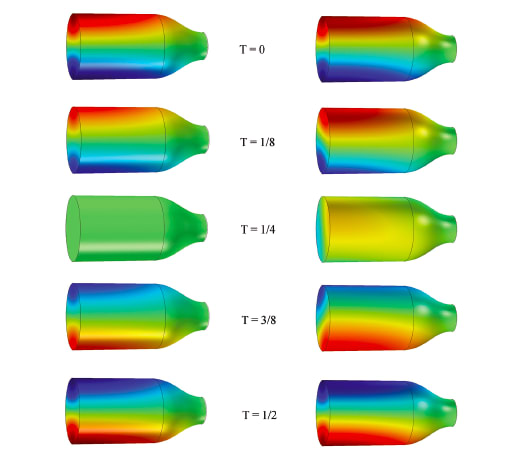
The eigenvalue solver produces complex eigenmodes and eigenvalues representing each acoustic mode and its complex conjugate. The real part of the complex eigenvalue represents the temporal damping of the acoustic mode, with the imaginary part defining the frequency of oscillation. The complex eigenvectors represent the spatial amplitude and phasing of the acoustic wave. Comparing the acoustic mode shapes derived using the classic homogeneous wave equation (Helmholtz equation) to those derived using the AVPE demonstrates the benefits of higher-fidelity models that correctly represent the underlying physics. Including mean flow terms in the AVPE accurately models the phase shift caused by the steady gas flow. Phasing is extremely important since combustion instability models make use of temporal and spatial integration of the acoustic eignvectors.
Utilizing COMSOL Multiphysics to simulate the rocket gas dynamics and acoustic eigenmodes provides a more accurate mode shape over previous techniques. The higher-fidelity acoustic representation is easily incorporated into combustion instability models to give rocket designers and engineers greater predictive capability. The inclusion of damping devices, such as baffles, or changes in operating conditions, can now be more accurately modeled before testing.
Continued Work
A more complete depiction of combustion instability includes rotational oscillations and thermal oscillations in conjunction with chamber acoustics. Rotational oscillations occur as a direct result of the acoustic oscillation, where thermal waves can also be present in the absence of acoustic fluctuation. Con tinued work will focus on solving the viscous rotational wave that accompanies all acoustic oscillations.
This article was written by Sean R. Fischbach, Marshall Space Flight Center/Jacobs ESSSA Group, MSFC, Huntsville, AL. For more information, visit www.nasa.gov/centers/marshall .
References
- F. S. Bloomshield, Lessons Learned in Solid Rocket Combustion Instability, 43rd AIAA Joint Propulsion Conference, AIAA-2007-5803, Cincinnati, OH, July 2007.
- J. C. French, Nozzle Acoustic Dynamics and Stability Modeling, Vol. 27, Journal of Propulsion and Power, 2011.
- R. K. Sigman and B. T. Zinn, A Finite Element Approach for Predicting Nozzle Admittances, Vol. 88, Journal of Sound and Vibration, 1983, pp. 117-131.
- L. M. B. C. Campos, On 36 Forms of the Acoustic Wave Equation in Potential Flows and Inhomogeneous Media, Vol. 60, Applied Mechanics Reviews, 2007, pp. 149-171.

