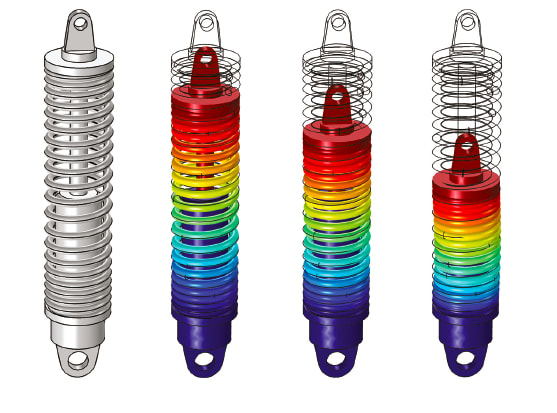
Shock absorbers are important parts of vehicles. The shock absorber is used to observe the vibrations from shock loads due to irregularities of the road surface, and operates without affecting the stability, steering, or handling of the vehicle. Generally, for light vehicles, cylindrical coil springs are used as suspension elements. The application described in this article attempts to analyze performance of a shock absorber with different suspension springs. This analysis includes comparative modeling and analysis of solid height, damping performance, oscillation capabilities of closed coil conical and cylindrical compression springs, and a suggested suitable design for improved performance.
Vehicle Suspension System

The suspension system of a ground vehicle is usually designed with the objectives of isolating the vehicle body from road irregularities, and maintaining wheel contact with the ground surface. Isolation is achieved by the use of helical compression springs and dampers, and by elastic mountings at the connections of the individual suspension components.

From a practical point of view, there are two major disturbances on a vehicle: road disturbances and load disturbances. Road disturbances have large magnitude in low frequency such as hills, and small magnitude in high frequency such as road roughness. Load disturbances include the variation of loads induced by accelerating, braking, and cornering. Therefore, a good suspension design is concerned with disturbance rejection from these disturbances to the outputs. Conventional suspension needs to be “soft” to insulate against road disturbances, and “hard” to insulate against load disturbances.
Therefore, shock absorber design is an art of compromise between these two goals. The main function of shock absorbers in a suspension system is to isolate the structure and occupants from shocks and vibrations generated by uneven road surfaces. The shock absorber requires an elastic resistance to absorb the road shocks — this is accomplished with suspension springs.
The primary objectives of a vehicle suspension system are:
- To provide good ride and handling performance. This is accomplished with vertical compliance providing chassis isolation, ensuring the wheels follow the road, and ensuring minimal tire load fluctuation.
- To ensure that proper steering is maintained during maneuvering. Wheels must be maintained at the proper position with respect to road surface.
- To ensure that the vehicle responds favorably to control forces produced by the tires during longitudinal braking, accelerating forces, lateral cornering forces, and braking and accelerating torques.
- To provide isolation from high-frequency vibration of tire excitation. This requires proper isolation in the suspension joint to prevent transmission of road noise to the vehicle body.
Suspension Springs
Springs are crucial suspension components on automobiles that are necessary to minimize the impacts and bumps due to uneven roads and provide a comfortable ride. The spring is defined as an elastic body whose function is to compress when loaded, and regain its original shape when the load is removed. Mechanical springs are used in shock absorbers to exert force, provide flexibility, and store or absorb energy. The force can be an axial push or pull, or it can be radial. The torque can be used to cause a rotation.
Springs can be classified according to the direction and characteristics of the forces exerted by the spring when it is deflected. Without any applied load, the spring’s height is called the free length. When a compression force is applied, the coils are pressed together until they touch each other. After compression, the compressed spring height is called the solid length. The main objectives of helical springs are to apply force, control motion, control vibration, and reduce impact.
Compression Springs
Compression springs are helical coil springs wound with spacing between the coils so they can be compressed from their free length to a shorter operating length. This allows the spring to store energy and provide a force or pressure. Some uses of compression springs include resisting the movement of another component, returning a component to a desired position, providing consistent pressure, and storing and releasing energy.
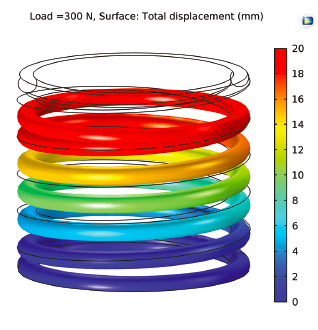
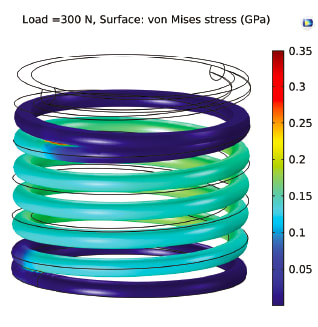
Cylindrical compression springs are wound in the form of a helix of a wire on cylindrical geometry. The major stresses produced are shear due to twisting. The applied load is parallel to the axis of spring. The cross section of the wire may be round, square, or rectangular. Figure 2 shows the cylindrical compression spring model used in this application. The cylindrical compression spring is rigidly attached with two circular rings at both ends.
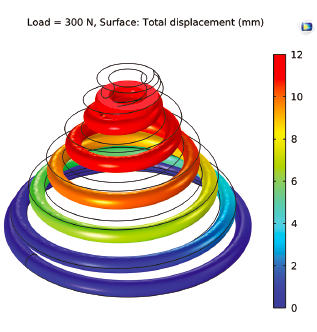
Conical compression springs are wound in the form of a helix of a wire on conical geometry. The major stresses produced are also shear due to twisting, and tensile and compressive stress due to bending. Figure 3 shows a conical compression spring design used in this experiment. In this design, both ends of the springs are rigidly attached with two different diameter circular rings.

Numerical Modeling Simulation
In this application, the damping performance of cylindrical and conical compression springs is analyzed numerically. The numerical model is developed with the solid mechanics interface of COMSOL Multiphysics software (COMSOL, Inc., Burlington, MA). A linear stationary analysis is performed to obtain desired deflection and stress at various loading conditions.
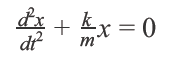
Figures 2 and 3 represent the CAD models of respective spring designs used in this investigation. Both models are designed to have same coil diameter, free length, number of active coils, and material properties.
- Material Density (⍴) = 7850 kg/m3
- Young’s Modulus (E) = 200 GPa
- Poisson’s Ratio (ν) = 0.33
Individual spring models are assumed to be fixed at the bottom end, and compressive force is applied to the top end. The radial deflection is neglected for the current application. A varying compressive load of 100 N to 2000 N is applied parametrically in the linear stationary study environment.
Governing Equation
The differential equation shown in Figure 12 (where x = Displacement, k = Spring Stiffness, and m = Loaded Mass) is implemented for both spring designs, and solved in the solid mechanics physics environment of COMSOL Multiphysics.
Results
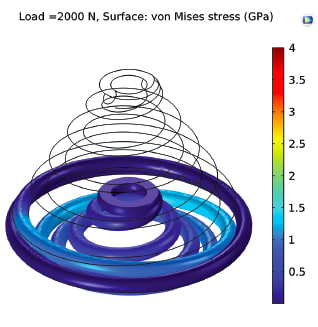
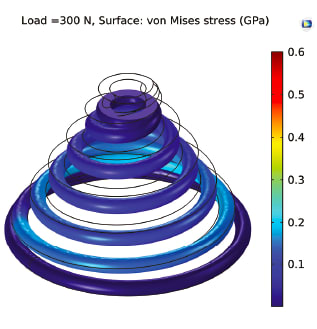
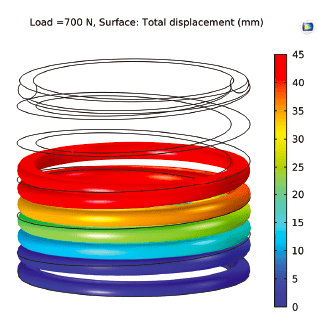
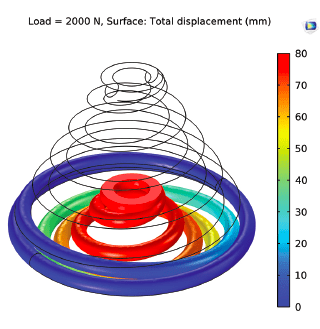
Simulation results (Figures 4-7) show maximum deflection and Von Mises stress values in both models for specified load parameters. The cylindrical spring design shows limited deflection of 45 mm at 700 N (Figure 8), while the conical spring operates at 2000 N with 80 mm deflection (Figure 10). The conical spring shows maximum compression, negative solid height, and better oscillations compared to the cylindrical spring.
This optimized conical spring design shows the potential to operate in harsh conditions compared to regular springs in a shock absorber. The conical compression spring design can offer superior lateral stability and ride comfort. Negative solid height can be achieved by conical compression springs in a shock absorber, which will help to reduce impacts. The conical spring design can provide better oscillation and wheel-to-ground contact. Nonlinear multiphysics study will be performed for structural design optimization, and development of energy-harvesting, low-cost, high-performance shock absorbers.
This article was written by Asutosh Prasad and Raj C Thiagarajan of ATOA Scientific Technologies, Bengaluru, India. For more information on the COMSOL products used in this project, visit http://info.hotims.com/61065-321 .

