The Signal-to-Noise Ratio (SNR) is a well-known and readily understood metric for data quality. Stated simply, SNR is the magnitude of the signal divided by the magnitude of the noise in the signal. The SNR can be determined by taking multiple identical measurements, and then dividing the mean value of these measurements, by the standard deviation, σ(λ):
Here the SNR is written as a function of the wavelength because it almost always varies from spectral channel to spectral channel. In practice, one rarely records multiple identical measurements to determine the SNR. Moreover, the SNR is dependent on several factors that may vary between scenes and deployments. Therefore, it is useful to understand the factors that impact the SNR and how one might optimize performance.
The Signal
The signal collected by a hyperspectral imager, σ(λ), in units of Joules, collected by each detector element (spatial, spectral channel), is calculated to a good approximation using the formula:
For optimal performance, the signal is near detector saturation. Therefore, it is worthwhile discussing each factor in this equation to understand how to obtain large signals and to understand the tradeoffs.
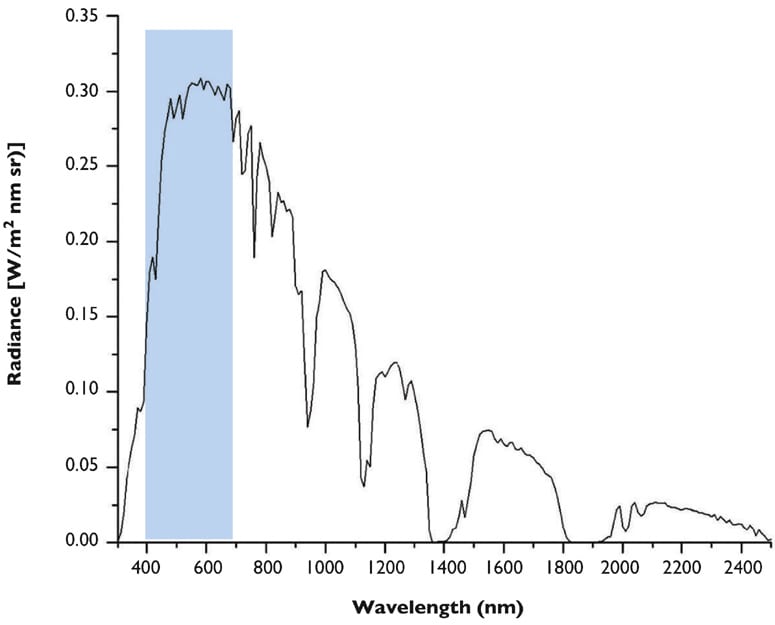
L(λ) is the at-sensor spectral radiance at wavelength in units of W/(m2 sr nm). In layman’s terms, this tells you the brightness of the light coming into the imager, usually from the object of interest. Thus, the information of interest is in this term. You can increase your Signal (and thus your SNR) with brighter illumination. Generally, the illumination changes with wavelength. For example, the signal from a Lambertian object with perfect reflectivity when illuminated by the sun in typical atmospheric conditions is shown in Figure 1. Note that illumination becomes weaker at both short (~400 nm) and long wavelengths, and thus the signal (and SNR) typically degrade at short and long wavelengths. The visible wavelength range is approximately 400-700 nm.
A D is the detector area in m2. This is the area for a channel, often the pixel area on the camera. Large pixel-area increases your signal, and pixel-binning effectively increases the pixel-area. Because it is complicated and expensive to integrate new cameras into a hyperspectral imager, this is usually not a parameter you adjust.
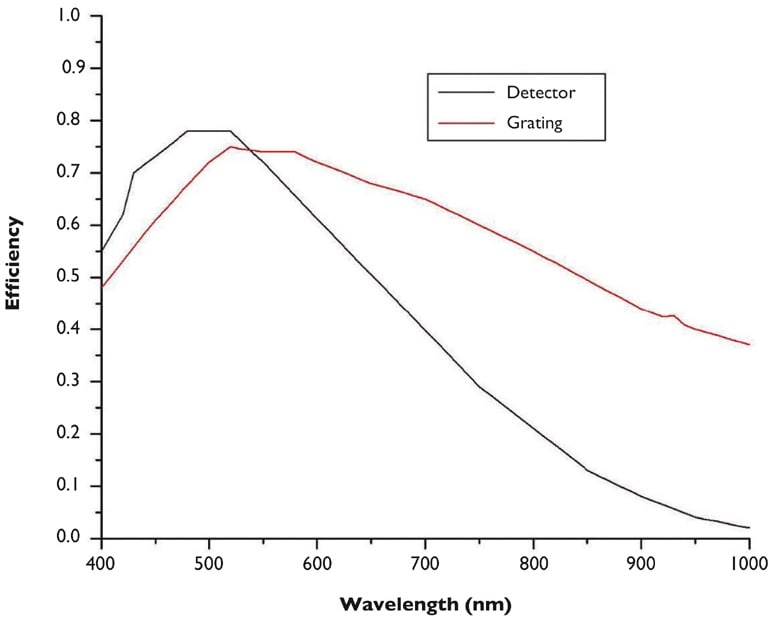
ε(λ) is the optical system efficiency which includes optical throughput of the lenses, the diffraction grating efficiency, and the detector quantum efficiency. The grating and detector efficiencies usually change significantly with wavelength and thus impact the wavelength dependence of the SNR. The overall efficiency is a product of the efficiencies listed above. Changing the efficiency requires changing components to the hyperspectral imager, which is not practical for most users.
Δλ is the optical bandwidth spread out across the detector area (pixel). This is another parameter determined by the instrument design, and therefore not adjustable for most users. In many cases, the optical bandwidth is narrower than needed, in which case it may make sense to bin spectral channels, as discussed below. Novel instrument designs can also be employed to adjust the bandwidth*.
Δt is the integration time (shutter) in seconds. This is one of the easiest parameters to adjust. The MAXIMUM integration time is 1/(frame rate). Thus, to increase signal (and SNR), one may: (1) decrease your frame rate and (2) then increase your shutter. A disadvantage of long integration times is slow frame-rates.
(f/#) is the imaging lens f-number, which is a measure of the instrument’s aperture. For maximum signal (and best SNR), one should set the f/# on the objective lens to the f/# of the instrument. (Alternatively, a higher f/# setting on your objective lens will provide a deeper depth of field.) Setting the objective f/# to a lower value than the instrument can lead to excess stray light, which will degrade the results.
The Noise. There are many sources of noise, and a detailed treatment is beyond the scope of this document. Fortunately, an abbreviated treatment is sufficient for most purposes, although some discussion is useful.
For the purposes of this discussion we assume:
The detectors are “photon detectors.” This includes conventional silicon CCD and CMOS cameras, InGaAs cameras for the 900-1,700 nm range, and longer-wavelength cameras that use MCT and InSb. It does NOT include, for example, micro-bolometers. This assumption means shot-noise is important (and often dominant), as discussed below.
The various noise sources are uncorrelated within a pixel and from pixel to pixel. For example, dark current noise does not correlate with read noise within a pixel, and the dark current noise in one pixel is independent of the dark current noise in any other pixel.
Uncorrelated noise sources do not add linearly. That is, for a given measurement one noise source may be large, another may be small or even negative. Taken together, the total mean noise, NT, from multiple uncorrelated noise sources is given by
where N x is the value of a particular noise source in units of electrons.
From a practical point of view, this characteristic simplifies noise modeling because one need only identify the largest few noise sources to adequately approximate the total noise. This can be understood by considering the total noise from two noise sources, of which the second is 30% as large as the first. Here,. Thus, one sees that the total noise is only slightly larger than the largest noise source.
Noise Sources
Shot Noise: Shot-noise arises due to variance in the signal itself and is equal to the square root of the number of electrons collected by the detector. The signal collected by a hyperspectral imager in units of electrons is given by, which is the signal collected in units of energy divided by the amount of energy per photon. Here h is Plank’s constant and c is the speed of light.
Dark Current Noise: The dark current is often provided by the detector vendor. It contributes to the signal desired by an amount equal to the dark current times the integration time, (iDark)Δt, where io ark is the dark current in units of electrons/s and Δt is the integration time. One should subtract the dark current from the recorded signal – this is not noise, just background that can be removed. The dark current noise is the variance in the dark current. Much like shot-noise, the dark current noise is equal to the square root of the dark current contribution,.
Read Noise: This noise source is typically provided by camera vendors and is a single contribution to the noise associated with every electronic read of the pixel.
Digitization (or Quantization) Noise: Most cameras used with hyperspectral imagers provide a digital output, usually between 8 and 16 bits. Because there are a range of signal inputs associated with each digitization value, uncertainty is introduced by the digitization process that leads to this noise source. Digitization noise, NDig, is given approximately by
where (Full Well) is the well depth of the detector in electrons (this assumes the analog to digital converter is adjusted so its maximum output corresponds to the full well depth), and B is the number of bits. Stated another way, this is the number of electrons associated with each digitization step divided by the square root of twelve. Warning: The digitization circuits may not be set so the maximum output corresponds to the full well, such as when a camera is in a “high gain” mode.
Other noise sources exist, but often the ones listed above are sufficient to accurately determine the SNR. Thermal noise becomes significant at the longer wavelengths in the SWIR and for wavelengths longer than the SWIR.
Signal-to-Noise Ratio (SNR)
Using the noise sources discussed above, the signal-to- noise ratio as a function of wavelength, SNR(λ), is calculated using the following equation:
where Nread is the read noise and all other parameters have been defined above. Before comparing this model to measured SNR, we consider some special cases.
Shot-Noise Limit: Because the shot-noise increases with signal, it becomes the dominant noise source in cases where one has a large signal. In this situation, the SNR is well-approximated by
which is the square root of the number of electrons collected by the sensor. Since, the largest signal that can be collected by a pixel in units of electrons is the full-well depth, one finds that the maximum possible SNR is approximately. This is why optimal performance is achieved by operating close to detector saturation.
For silicon cameras, pixel full-well depths are typically a few tens-of-thou-sands, which means the highest possible SNRs for a single pixel are in the low hundreds. InGaAs and MCT cameras often have full-well depths of around one-million electrons, resulting in maximum SNRs of around one-thousand.
Binning: The spectral resolution of hyperspectral imagers is often better than required, but the SNR may well be lacking. Therefore, it is often advantageous to bin channels to improve the SNR. However, care must be exercised to take full advantage of binning.
In principle, the SNR achieved by binning to BN channels is given by:
where BN is the number of channels binned and λBN is the wavelength label for the binned channels, typically the central wavelength of the binned spectral range. All noise sources are assumed to be uncorrelated and all channels (pixels) are assumed to have identical noise properties. For wavelength channels that are sufficiently close in wavelength, one would expect their values to be approximately the same. Consequently,
With this approximation,
Thus, the SNR increases by approximately the square root of the number of bins, as one would expect. The maximum SNR with binning occurs when operating near saturation, and is on the order of
Binning Warning: It appears some cameras that provide “on chip” binning, bin the electrons before the analog to digital converter, but do not change the saturation level for the analog to digital converter. Consequently, the effective full well per pixel actually decreases by a factor of the bin number, BN. In this circumstance, the maximum possible SNR is not improved by binning, although actual SNR may be improved when operating well below saturation.
SNR: Measurements and Model
The experimental SNR was determined by recording multiple measurements of a calibrated integrating sphere with a Pika XC2 imaging spectrometer from Resonon. Using a central spatial channel, the mean value and standard deviation were determined for each spectral band. The SNR for each band was then calculated by dividing the mean by the standard deviation.
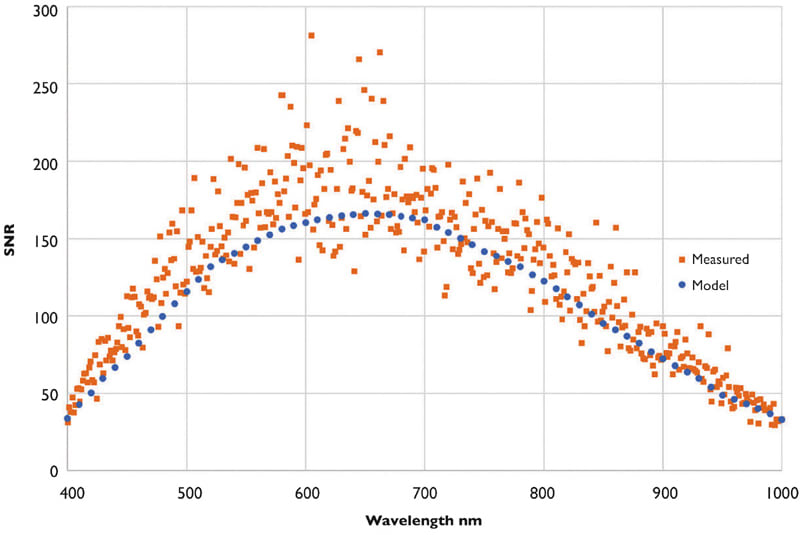
The SNR was modeled using the approach described above, with the integration time adjusted to match the setting used for the measurements and using the known radiance values from the integrating sphere. Plots of the SNR, measured and modeled, are shown in Figure 3.
Perhaps the first thing one notices is that the measured SNR exhibits considerable fluctuation. This is not surprising, as the noise is variable and relatively small; therefore when one divides a relatively large signal value by a small, variable quantity, the result exhibits fluctuations. Second, one notes the model results match the measured values fairly well.
Summary
A model for the SNR for hyperspectral imagers has been discussed. This model illustrates what quantities are important to achieving a large SNR as well as possible pitfalls. A comparison of the model and measured results is quite reasonable, indicating SNR performance can be reliably modeled for real-world applications.
References
- Rand Swanson, William S. Kirk, Guy C. Dodge, Michael Kehoe, and Casey Smith “Anamorphic imaging spectrometers”, Proc. SPIE 10980, Image Sensing Technologies: Materials, Devices, Systems, and Applications VI, 1098005 ( 13 May 2019 ).
This article was written by Rand Swanson, President, Resonon, Inc., (Bozeman, MT). For more information, visit here .