3D imaging technology has come a long way from its roots in academic research labs, and thanks to innovations in sensors, decreasing cost of components, and the emergence of 3D functions in software libraries, 3D vision is now appearing in a variety of machine automation applications. From vision-guided robotic bin-picking to high-precision metrology, the latest generation of processors can now handle the immense data sets and sophisticated algorithms required to extract depth information and quickly make decisions.

There are several ways to calculate depth information using 2D camera sensors or other optical sensing technologies, each of which has its own set of tradeoffs and benefits, and the choice of technique often depends on the application itself. Common techniques for 3D vision include stereovision, laser triangulation, time of flight, and projected light. This article will focus on stereovision, which uses the disparity between images from multiple cameras to extract depth information.
Stereovision Functions
Binocular stereovision algorithms can be used to calculate depth information from multiple cameras. By using calibration information between two cameras, the new algorithms can generate depth images, providing richer data to identify objects, detect defects, and guide robotic arms on how to move and respond.
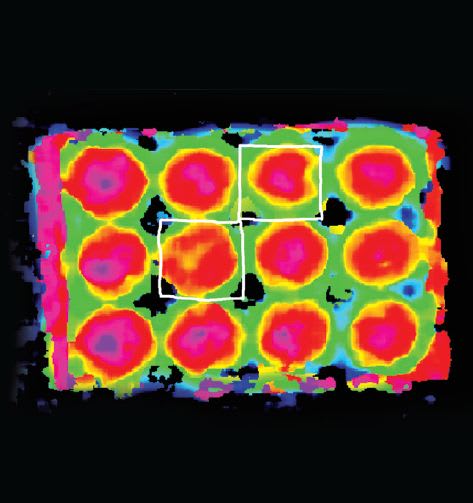
A binocular stereovision system uses exactly two cameras. Ideally, the two cameras are separated by a short distance, and are mounted almost parallel to one another. In the example shown in Figure 1, a box of spherical chocolates is used to demonstrate the benefits of 3D imaging for automated inspection. After calibrating the two cameras to know the 3D spatial relationship, such as separation and tilt, two different images are acquired to locate potential defects in the chocolate. Using 3D stereovision algorithms, the two images can be combined to calculate depth information and visualize a depth image.
While difficult to characterize using traditional two-dimensional functions, the 3D depth image shows that two of the chocolates are not spherical enough to pass the high quality standards. The image in Figure 2 shows a white box around the defects that have been identified.
One important consideration when using stereovision is that the computation of the disparity is based on locating a feature from a line of the left image, and the same line of the right image. To be able to locate and differentiate the features, the images need to have sufficient detail, and the objects sufficient texture or non-uniformity. To obtain better results, one may need to add this needed detail by illuminating the scene with structured lighting.
Finally, binocular stereovision can be used to calculate the 3D coordinates (X,Y,Z) of points on the surface of an object being inspected. These points are often referred to as point clouds or cloud of points. Point clouds are very useful in visualizing the 3D shape of objects and can also be used by other 3D analysis software.
How Stereovision Works
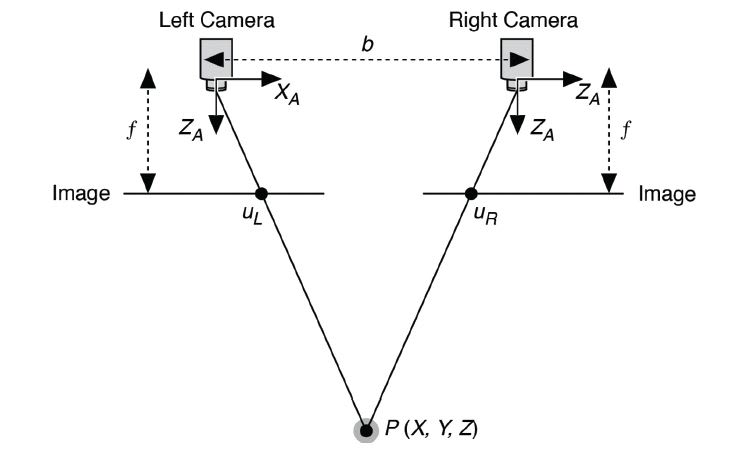
To better illustrate how binocular stereovision works, Figure 3 shows the diagram of a simplified stereovision setup, where both cameras are mounted perfectly parallel to each other, and have the exact same focal length.
The variables in Figure 3 are: b is the baseline, or distance between the two cameras.
f is the focal length of a camera.
XA is the X-axis of a camera.
ZA is the optical axis of a camera.
P is a real-world point defined by the coordinates X, Y, and Z.
uL is the projection of the real-world point P in an image acquired by the left camera.
uR is the projection of the real-world point P in an image acquired by the right camera.
Since the two cameras are separated by distance “b,” both cameras view the same real-world point P in a different location on the two-dimensional images acquired. The X-coordinates of points uL and uR are given by:
uL = f * X/Z
and
uR = f * (X-b)/Z
Distance between those two projected points is known as “disparity” and we can use the disparity value to calculate depth information, which is the distance between real-world point “P” and the stereo vision system.
disparity = uL – uR = f * b/z
depth = f * b/disparity
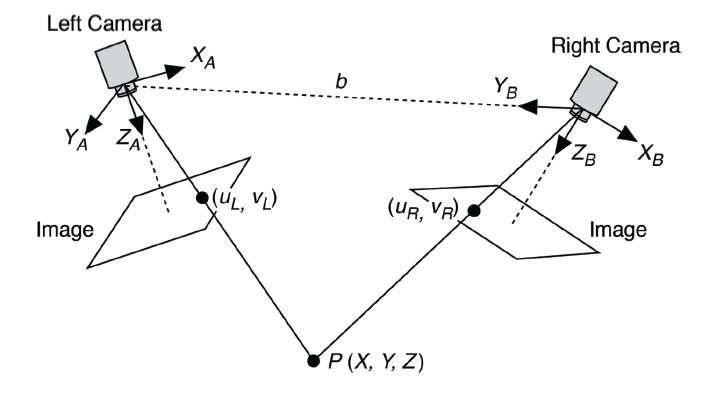
In reality, an actual stereovision setup is more complex and would look more like the typical system shown in Figure 4, but all of the same fundamental principles still apply.
The ideal assumptions made for the simplified stereovision system cannot be made for real-world stereovision applications. Even the best cameras and lenses will introduce some level of distortion to the image acquired, and in order to compensate, a typical stereovision system also requires calibration. The calibration process involves using a calibration target — for example, a grid of dots or a checkerboard — and acquiring images at different angles to calculate image distortion, as well as the exact spatial relationship between the two cameras.
In order to optimize the accuracy of a stereovision system setup, and accurately relate calculated image disparity to true depth data, there are several considerations and parameters to keep in mind.
For a simple stereo system, the depth of a point (z) is given by:
Z = f * b/d
where f is the focal length, b is the baseline, or distance between the cameras, and d the disparity between corresponding points.
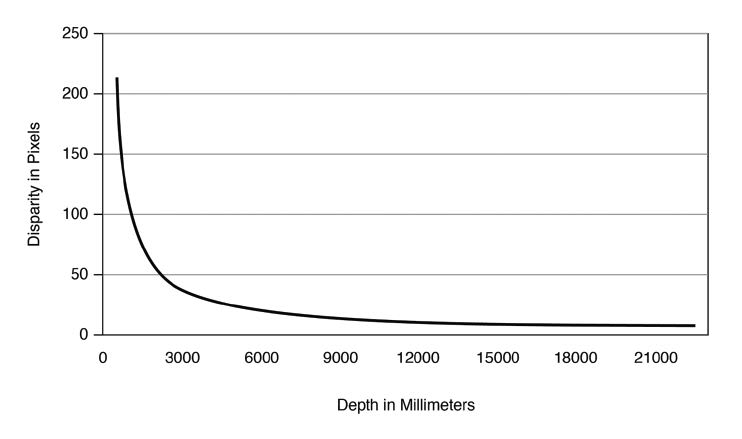
When relating depth to disparity, it is important to note that as depth decreases, disparity increases exponentially, as illustrated in Figure 5.
Depth resolution refers to the accuracy with which a stereovision system can estimate changes in the depth of a surface. Depth resolution is proportional to the square of the depth and the disparity resolution, and is inversely proportional to the focal length and the baseline, or distance between the cameras. Good depth resolution requires a large baseline value, a large focal length value, and a small depth value for a given disparity resolution.
Stereovision Applications
Stereovision is well suited to applications that require locating objects or obstacles, and this location data can be used to guide the movement of a robot or robotic arm. For navigating auto - nomous vehicles, depth information is used to measure the size and distance of obstacles for accurate path planning and obstacle avoidance. Stereovision systems can provide a rich set of 3D information for navigation applications, and can perform well even in changing light conditions.
A stereovision system is also useful in robotic industrial automation of tasks such as bin-picking or depalletization. A bin-picking application requires a robot arm to pick a specific object from a container that holds several different kinds of parts. A stereovision system can provide an inexpensive way to obtain 3D information and determine which parts are free to be grasped. It can also provide precise locations for individual products in a crate.
This article was written by Dinesh Nair, Chief Architect at National Instruments, Austin, TX. For more information, Click Here .

