Modified Taguchi techniques of robust design optimization are used in an innovative method of training artificial neural networks — for example the network shown in the figure. As in other neural-network-training methods, the synaptic weights (strengths of connections between neurons) are adjusted iteratively in an effort to reduce a cost function, which is usually the sum of squared errors between the actual network outputs and the prescribed (correct) network outputs for training sets of inputs. However, this method offers advantages over older methods, as explained below.
Heretofore, the most popular neural-network-training methods have been based, variously, on gradient-descent (GD) techniques or genetic algorithms (GAs). GD techniques are local search/ optimization techniques; in a typical case, a GD technique leads to a local minimum of the cost function, which may not be the desired global minimum. Moreover, GD learning is slow, typically requiring thousands of iterations. GA learning involves global searches but is also slow, typically requiring hundreds of generations with hundreds of individuals in the population. The present innovative method involves global searches and enables a neural network to learn much faster (equivalently, in fewer iterations) than do GD- and GA-based methods.
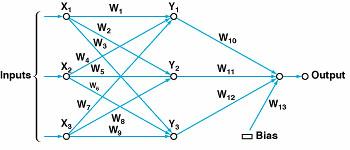
In the present method, each of the N synaptic weights is treated as one of N design parameters to be optimized by Taguchi techniques. At each iteration, a number, M, of trial network designs are considered. In each design, each parameter is set at one of three distinct arbitrary levels. The various designs considered at each iteration are thus represented by M sets of N parameters each, each set being a distinct combination of the three levels. The ensemble of all M trial designs considered at each iteration can thus be represented by an N ×M rectangular array. For example, the table shows an array of M= 27 trial sets of N = 13 parameters each for the neural network illustrated in the figure.
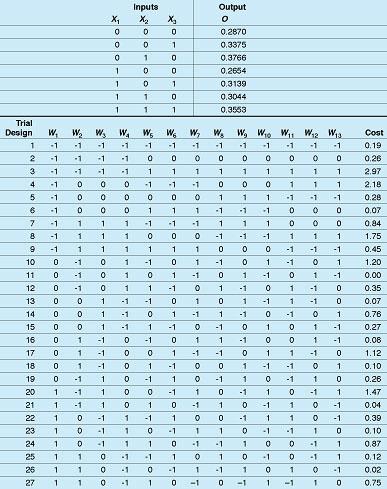
The cost is computed for each trial design. For each parameter, one computes three different cumulative costs, each comprising the sum of all costs for one of the three parameter levels. The three cumulative costs are compared. Then the search range for the parameter is narrowed and is shifted toward whichever level gave the lowest cumulative cost; that is, three shifted, more-closely-spaced levels of the parameter are chosen for the trial designs on the next iteration.
The process is repeated until the parameters converge on values that make the cost acceptably small. Typically, the search range for each parameter can be narrowed by half on each iteration, so that the intervals containing the solution can shrink by a factor of about 103 in only ten iterations. Thus, learning time is shortened considerably, relative to GD- and GA-based methods.
This work was done by Julian O. Blosiu and Adrian Stoica of Caltech forNASA's Jet Propulsion Laboratory. For further information, access the Technical Support Package (TSP) free on-line at www.techbriefs.com under the Mathematics and Information Sciences category, or circle no. 115 on the TSP Order Card in this issue to receive a copy by mail ($5 charge).
NPO-20018
This Brief includes a Technical Support Package (TSP).

Training of neural networks by modified Taguchi techniques
(reference NPO20018) is currently available for download from the TSP library.
Don't have an account?
Overview
The document presents an innovative method for training artificial neural networks (NN) that significantly reduces learning time by employing modified Taguchi techniques of robust design optimization. Authored by Julian Blosiu and Adrian Stoics at the Jet Propulsion Laboratory, this approach addresses the limitations of traditional neural network training methods, which often rely on gradient descent (GD) or genetic algorithms (GA).
Traditional GD techniques are local search methods that can lead to local minima of the cost function, which is typically the sum of squared errors between actual and desired outputs. This process is often slow, requiring thousands of iterations to converge. On the other hand, GA methods involve global searches but are also computationally expensive, necessitating hundreds of generations with numerous individuals in the population. Both methods are inadequate for real-time applications where fast learning is critical.
The proposed method utilizes a global search mechanism that allows for quicker learning by treating each synaptic weight as a design parameter to be optimized using Taguchi techniques. At each iteration, multiple trial network designs are evaluated, with each design representing a distinct combination of parameter levels. This iterative process employs orthogonal arrays to systematically explore the parameter space, leading to a more efficient search for optimal weight values.
The document highlights that the new learning algorithm can drastically reduce the time required for neural network training. It notes that the interval containing the solution can shrink by three orders of magnitude every ten iterations, showcasing the method's effectiveness. This rapid convergence is particularly beneficial for applications requiring real-time processing and decision-making.
In summary, the document outlines a novel approach to neural network training that leverages robust design optimization techniques to enhance learning speed and efficiency. By overcoming the limitations of traditional methods, this innovative strategy holds promise for advancing artificial intelligence applications, making it a significant contribution to the field of neural networks. The research is documented in a technical support package for NASA, emphasizing its relevance and potential impact on future technological developments.

