The conical-domain model is a computational model, now undergoing development, for estimating ionospheric delays of Global Positioning System (GPS) signals. Relative to the standard ionospheric delay model described below, the conical-domain model offers improved accuracy.
In the Wide Area Augmentation System (WAAS) of the United States, slant ionospheric delay errors and confidence bounds are derived from estimates of vertical ionospheric delay modeled on a grid at regularly spaced intervals of latitude and longitude. The estimate of vertical delay at each ionospheric grid point (IGP) is calculated from a planar fit of neighboring slant delay measurements, projected to vertical using a standard, thin-shell model of the ionosphere. Interpolation on the WAAS grid enables estimation of the vertical delay at the ionospheric pierce point (IPP) corresponding to any arbitrary measurement of a user. (The IPP of a given user’s measurement is the point where the GPS signal ray path intersects a reference ionospheric height.) The product of the interpolated value and the user’s thinshell obliquity factor provides an estimate of the user’s ionospheric slant delay.
Two types of error that restrict the accuracy of the thin-shell model are absent in the conical domain model: (1) error due to the implicit assumption that the electron density is independent of the azimuthal angle at the IPP and (2) error arising from the slant-to-vertical conversion. At low latitudes or at mid-latitudes under disturbed conditions, the accuracy of SBAS systems based upon the thin-shell model suffers due to the presence of complex ionospheric structure, high delay values, and large electron density gradients. Interpolation on the vertical delay grid serves as an additional source of delay error.
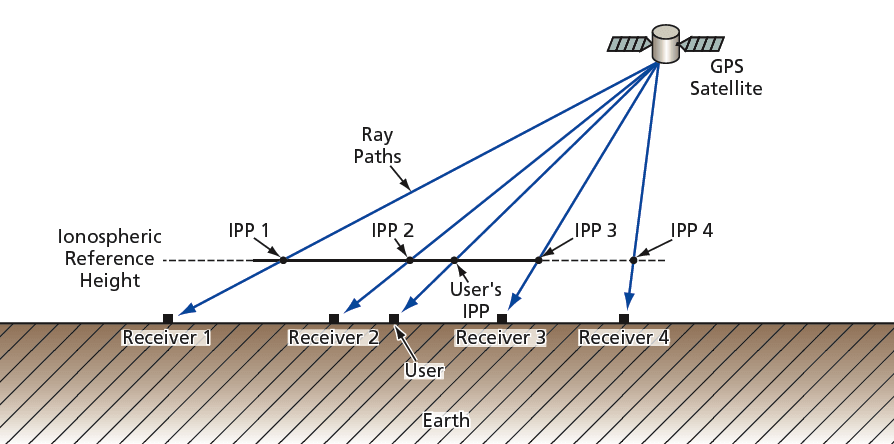
The conical-domain model permits direct computation of the user’s slant delay estimate without the intervening use of a vertical delay grid. The key is to restrict each fit of GPS measurements to a spatial domain encompassing signals from only one satellite. The conical domain model is so named because each fit involves a group of GPS receivers that all receive signals from the same GPS satellite (see figure); the receiver and satellite positions define a cone, the satellite position being the vertex. A user within a given cone evaluates the delay to the satellite directly, using (1) the IPP coordinates of the line of sight to the satellite and (2) broadcast fit parameters associated with the cone.
The conical-domain model partly resembles the thin-shell model in that both models reduce an inherently four-dimensional problem to two dimensions. However, unlike the thin-shell model, the conical domain model does not involve any potentially erroneous simplifying assumptions about the structure of the ionosphere. In the conical domain model, the initially four-dimensional problem becomes truly two-dimensional in the sense that once a satellite location has been specified, any signal path emanating from a satellite can be identified by only two coordinates; for example, the IPP coordinates. As a consequence, a user’s slant-delay estimate converges to the correct value in the limit that the receivers converge to the user’s location (or, equivalently, in the limit that the measurement IPPs converge to the user’s IPP).
This work was done by Lawrence Sparks, Attila Komjathy, and Anthony Mannucci of Caltech for NASA’s Jet Propulsion Laboratory.
The software used in this innovation is available for commercial licensing. Please contact Karina Edmonds of the California Institute of Technology at (626) 395-2322. Refer to NPO-40930.
This Brief includes a Technical Support Package (TSP).

Conical-Domain Model for Estimating GPS Ionospheric Delays
(reference NPO-40930) is currently available for download from the TSP library.
Don't have an account?
Overview
The document discusses the Conical Domain Model for estimating ionospheric delays in Global Positioning System (GPS) signals, as presented in NASA's Technical Support Package NPO-40930. The primary goal of satellite-based augmentation systems (SBAS), such as the United States' Wide Area Augmentation System (WAAS), is to enhance the accuracy and integrity of user position estimates derived from GPS measurements. The ionosphere is identified as the largest source of error for single-frequency GPS users, necessitating improved methods for estimating ionospheric delays.
Traditional approaches, like the thin shell model, simplify the inherently four-dimensional problem of ionospheric delay estimation by reducing it to two dimensions. However, this model introduces significant errors due to assumptions about electron density and the slant-to-vertical conversion process. These errors can be particularly problematic at low latitudes or during disturbed conditions, where complex ionospheric structures and high electron density gradients exist. The thin shell model's reliance on grid interpolation further compounds these inaccuracies, making it insufficient for precise navigation, especially in equatorial regions.
The Conical Domain Model offers a novel approach by allowing direct computation of a user's slant delay estimate without the need for a vertical delay grid. This model confines the analysis to a conical domain defined by the satellite's position, with the satellite at the cone's vertex. By focusing on the ionospheric pierce point (IPP) coordinates and the line-of-sight to the satellite, the model eliminates the errors associated with grid interpolation and the thin shell model's assumptions.
The document emphasizes that the conical domain approach not only reduces sources of error but also enhances the accuracy of slant delay estimates as the receivers converge to the user's location. This method represents a significant advancement in ionospheric delay estimation, promising improved performance for SBAS systems and more reliable GPS navigation, particularly in challenging environments.
In summary, the Conical Domain Model presents a sophisticated alternative to traditional methods for estimating ionospheric delays, addressing the limitations of the thin shell model and grid interpolation. This innovation is crucial for ensuring the integrity and accuracy of GPS-based navigation systems, especially in regions where ionospheric conditions are complex.

