A relatively simple algorithm, devised for use in an image-data-compression application, partitions a rectangular pixelated image (or any other rectangle on which a regular rectangular grid has already been superimposed) into a specified number of smaller rectangles, hereafter denoted segments. The algorithm has the following properties:
- No floating-point operations are needed.
- The segments tend to be nearly square (in the sense that their widths and heights in pixel units tend to be nearly equal).
- The segments tend to have nearly equal areas.
- The algorithm yields valid results (no zero-width or zero-height segments) as long as the specified number of segments, s, does not exceed the number of pixels (equivalently, the number of grid cells).
{ntbad}The inputs to the algorithm are the positive integer s plus the positive integers h and w, denoting the height and width, respectively, of the rectangle in pixel units. The limit on s for a valid result is given by s ≤ wh.
The output of the algorithm is characterized by, and can be described completely in terms of, several parameters that are illustrated by the example shown in the figure. The segments are arranged in r rows. A top region of the rectangle contains segments arranged in c columns. A possible bottom region contains segments arranged in c + 1 columns. The top region has height ht and contains rt rows of segments. The first rt0 rows of segments in the top region have height yt; the remaining rows (if any) in the top region have height yt + 1. The first ct0 columns in the top region have width xt; any remaining columns in the top region have width xt + 1. Similarly, the first rb0 rows in the bottom region have height yb, and the remaining rows in the bottom region have height yb + 1, while the first cb0 columns in the bottom region have width xb and the remaining columns in the bottom region have width xb + 1.
The steps of the algorithm are the following: First, r is computed. If h > (s – 1)w then r = s. Otherwise, r is the unique positive integer that satisfies (r – 1)rw < hs ≤ (r+1)rw. Some of the other parameters are computed as follows:
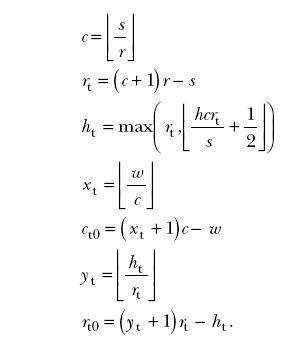
If rt < r, so that there is a bottom region, then the remaining parameters are computed as follows:
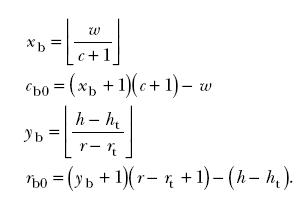
It has been verified by straightforward algebraic analysis of these equations that the algorithm has the properties mentioned in the first paragraph.
This work was done by Matthew Klimesh and Aaron Kiely of Caltech for NASA's Jet Propulsion Laboratory. For further information, access the Technical Support Package (TSP) free on-line at www.techbriefs.com/tsp under the Information Sciences category.
This software is available for commercial licensing. Please contact Don Hart of the California Institute of Technology at (818) 393- 3425. Refer to NPO-30479.
This Brief includes a Technical Support Package (TSP).

Partitioning a Gridded Rectangle Into Smaller Reactangles
(reference NPO30479) is currently available for download from the TSP library.
Don't have an account?
Overview
The document titled "Partitioning a Gridded Rectangle Into Smaller Rectangles" is a technical support package from NASA's Jet Propulsion Laboratory, detailing an algorithm for dividing a rectangle into smaller rectangles. The primary inputs to the algorithm are positive integers representing the width (w), height (h), and the desired number of segments (s). The algorithm ensures that the number of segments does not exceed the area of the rectangle, adhering to the condition ( s \leq wh ).
The algorithm aims to produce a partition consisting of ( s ) smaller rectangles arranged in ( r ) rows and ( c ) columns. The top region of the rectangle contains segments arranged in ( c ) columns, while a possible bottom region may contain segments arranged in ( c + 1 ) columns. The height of the top region is denoted as ( h_t ), which is further divided into ( r_t ) rows, with some rows having a height of ( y_t ) and others ( y_t + 1 ). The bottom region follows a similar structure.
A key aspect of the algorithm is the calculation of ( r ), which is determined based on the relationship between the height and the desired number of segments. If the height exceeds a certain threshold, ( r ) is set to ( s ); otherwise, it is calculated to satisfy specific inequalities. The algorithm also ensures that the produced segments are nearly square, which is beneficial for compression purposes, as square regions have smaller perimeters and thus more neighboring pixels, allowing for better correlation and compression efficiency.
The document emphasizes the advantages of this partitioning method over simpler approaches, such as dividing the image into smaller images. It highlights that the proposed method achieves better decorrelation, minimizes noticeable boundaries between segments, and maintains consistent image quality across segments.
In summary, this technical support package provides a comprehensive overview of an algorithm designed for partitioning a rectangle into smaller rectangles, with applications in image processing and data compression. It outlines the mathematical foundations, properties, and benefits of the algorithm, making it a valuable resource for researchers and practitioners in aerospace-related fields and beyond. Further information and assistance can be accessed through NASA's Scientific and Technical Information Program Office.

