An improved approach to the mathematical modeling of feedback control of thermal networks has been devised. Heretofore software for feedback control of thermal networks has been developed by time-consuming trial-and-error methods that depend on engineers' expertise. In contrast, the present approach is a systematic means of developing algorithms for feedback control that is optimal in the sense that it combines performance with low cost of implementation. An additional advantage of the present approach is that a thermal engineer need not be expert in control theory.

Thermal networks are lumped-parameter approximations used to represent complex thermal systems. Thermal networks are closely related to electrical networks commonly represented by lumped-parameter circuit diagrams. Like such electrical circuits, thermal networks are mathematically modeled by systems of differential-algebraic equations (DAEs) — that is, ordinary differential equations subject to a set of algebraic constraints. In the present approach, emphasis is placed on applications in which thermal networks are subject to constant disturbances and, therefore, integral control action is necessary to obtain steady-state responses.

The Time-Dependent Offsets of Four Nodes of a 9-node network were computed in a numerical test of optimal- and decentralized-control laws. Both control laws yield smooth temperature histories, without oscillations or large overshoots, and both require about the same amount of time to achieve nearly zero offset (where offset as used here signifies the difference between the actual and desired temperatures of a given node).
The mathematical development of the present approach begins with the derivation of optimal integral-control laws via minimization of an appropriate cost functional that involves augmented state vectors. Subsequently, classical variational arguments provide optimality conditions in the form of the Hamiltonian equations for the standard linear-quadratic- regulator (LQR) problem. These equations are reduced to an algebraic Riccati equation (ARE) with respect to the augmented state vector. The solution of the ARE leads to the direct computation of the optimal proportional- and integral- feedback control gains.

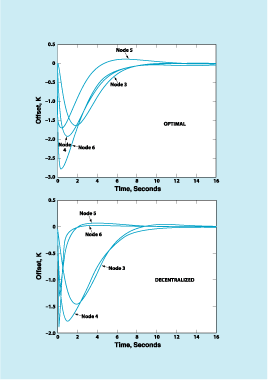
In cases of very complex networks, large numbers of state variables make it difficult to implement optimal controllers in the manner described in the preceding paragraph. Therefore, another important element of the present approach is consideration of decentralized control (that is, the use of nominally suboptimal controllers, each affecting only part of the network). Numerical tests of an algorithm that computes feedback gains for decentralized control have shown that the performances of the decentralized controllers are comparable to the performances of the corresponding optimal controllers (see figure). In particular, it was observed that decentralized controllers might require a little more energy than their optimal counterparts; however, this is a small price to pay for the simplification of controller structures that can be achieved. Further, the lower cost of implementation of much simpler feedback loops in decentralized control outweighs the extra amount of energy that decentralized controllers might require.

This work was done by Miltiadis Papalexandris of Caltech for NASA's Jet Propulsion Laboratory. For further information, access the Technical Support Package (TSP) free on-line at www.techbriefs.com/tsp under the Information Sciences category.

This software is available for commercial licensing. Please contact Don Hart of the California Institute of Technology at (818) 393-3425. Refer to NPO-30354.

Topics:
Computer software and hardware Data management Historical reference Information Technology Logistics Mathematical models Simulation and modeling
This Brief includes a Technical Support Package (TSP).
Document cover
Optimal Feedback Control of Thermal Networks

(reference NPO-30354) is currently available for download from the TSP library.

Don't have an account?

Magazine cover
NASA Tech Briefs Magazine

This article first appeared in the February, 2003 issue of NASA Tech Briefs Magazine (Vol. 27 No. 2).

Read more articles from the archives here.

Overview

The document titled "Optimal Feedback Control of Thermal Networks" is a Technical Support Package prepared under the sponsorship of NASA, specifically by the Jet Propulsion Laboratory (JPL). It outlines a novel approach to feedback control in thermal systems, particularly relevant for applications in spacecraft, such as the Next Generation Space Telescopes.

The primary innovation presented in this work is the development of algorithms and software that facilitate optimal feedback control of thermal networks. This approach is distinguished from traditional methods, which often rely on empirical trial-and-error techniques. The systematic methodology proposed in this document leverages recent advancements in control theory, allowing for a more efficient and effective means of managing thermal systems.

Key aspects of the document include:

  1. Novelty and Problem Statement: The work addresses the challenges faced in active thermal control of spacecraft, where complex thermal networks can involve numerous state variables, complicating the implementation of optimal controllers. The document emphasizes the need for a more structured approach to thermal control that does not depend on the thermal engineer's expertise in control theory.

  2. Solution Overview: The proposed solution involves optimal feedback control, and for larger systems, decentralized control is suggested. This decentralized approach utilizes nominally suboptimal controllers that manage only parts of the network, making it easier to implement in complex scenarios.

  3. Advantages: The new method computes optimal feedback control transparently, meaning that thermal engineers can utilize it without needing extensive knowledge of control theory. This not only saves time but also enhances efficiency and reduces costs associated with thermal management.

  4. Technical Disclosure: The document outlines the motivation behind the research, which is to improve the active thermal control of spacecraft. It also highlights the advantages of the proposed method over existing empirical approaches, which are often time-consuming and inefficient.

  5. Future Work: The document references an upcoming publication in the ASME Journal of Dynamic Systems, Measurement & Control, which will provide further details on the methodology and its applications.

In summary, this Technical Support Package presents a significant advancement in the field of thermal control for aerospace applications, offering a systematic and efficient approach that could greatly enhance the performance and reliability of thermal management systems in spacecraft.