A class of finite-impulse-response (FIR) digital filters has been developed to perform certain frequency-limiting, decimation, and differentiation (with respect to time) functions on a time series of data samples. The method is implemented by use of design equations that contain parameters that can be adjusted to obtain the desired functionality while limiting such undesired effects as aliasing and gain ripple. The original application is processing of a time series of raw range data from the proposed Gravity Recovery and Climate Experiment (GRACE), in which microwave phase tracking between two small spacecraft orbiting the Earth would yield the time-tagged raw range data, which would be processed to extract information on the structure of the gravitational field of the Earth. The method is general enough to be applicable in other situations that involve similar signal-processing requirements.
Consider a time series wherein Ri' denotes the raw datum at the jth sampling period. One seeks an FIR filter that can be convolved with the raw data in the time domain over a time window of an odd number, Nf, of sampling periods to obtain low-pass filtering plus decimation by a factor of Nf. The low-pass filtered, decimated time series is to be given by
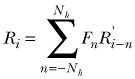where the Fn terms are the FIR filter coefficients and Nh = (Nf –1)/2. One also seeks low-pass-filtering and decimating FIR filters 
and 
to obtain the first and second derivatives of the data with respect to time (range rate and range acceleration in the original application). The corresponding equations are
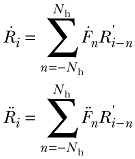
Each FIR filter is required to differentiate to the desired order and to exhibit a nearly rectangular low-pass frequency response. To prevent aliasing of out-of-band noise into the desired low-pass band, the low-pass cutoff frequency should be set at or near the applicable Nyquist value, which is half the output data sampling frequency. The well-known window-function approach is used to formulate the FIR filter. The time-domain window function consists of a rectangular time-domain window self-convolved Nc times. The frequency-domain response of such a time-domain window is approximately given by a simple closed-form expression of the form [sin x/x]Nc+1. This class of filters is classified as CRN filters designating N convolutions of a rectangle.
In designing the filter, one must choose values for the nominal cutoff frequency (bandwidth), for Nc, and for the filter length Tf = Nf/fs (where fs is the raw-data sampling frequency). The filter is first constructed in the frequency domain by convolving the desired rectangular low-pass frequency response with the known discrete Fourier transform, [sin x/x]Nc+1, of the selected Nc-self-convolution time-domain window function. The result of this convolution is then discrete-Fourier-transformed to the time domain to obtain the FIR coefficients. The advantage of this class of FIR filter is that the frequency-domain response can be approximately assessed "in advance" on the basis of the simple [sin x/x]Nc+1 function. Further differentiation can be easily applied by multiplying by 2π f in the frequency domain.
The upper part of the Figure 1 depicts the FIR coefficients and frequency response of a range filter designed according to this method for a test case, using Nc = 6. As one would expect, the FIR amplitude vs. time resembles a sin(x)/x function, except that it tapers toward zero in the outer time regions. This taper is caused by the window function. The lower part of Figure 1 shows the predicted frequency response of the range filter. Figure 2 depicts the FIR coefficients of a range-rate (first-derivative) filter for the same test case.
This work was done by J. B. Thomas of Caltech for NASA's Jet Propulsion Laboratory. For further information, access the Technical Support Package (TSP) free on-line at www.nasatech.com/tsp under the Information Sciences category.
NPO-20643
This Brief includes a Technical Support Package (TSP).
A method for designing low-pass FIR digital filters
(reference NPO-20643) is currently available for download from the TSP library.
Don't have an account?
Overview
The document presents a technical support package from NASA, focusing on the design of low-pass Finite Impulse Response (FIR) digital filters. This work is particularly relevant for processing time series data, with applications in missions such as the Gravity Recovery and Climate Experiment (GRACE). The primary goal is to develop a method that allows for the effective extraction of meaningful signals from noisy data, which is crucial in various scientific and engineering fields.
The document outlines the theoretical foundations of FIR filter design, emphasizing the importance of careful filter design to achieve desired performance characteristics. It discusses the dual-l-way (biased) range values that are to be produced at a nominal rate of 10 samples per second (S/s), which is essential for accurate data processing in space missions. The design process includes considerations of bandwidth, gain normalization, and the frequency response of the filters, ensuring that the filters can adequately suppress unwanted noise while preserving the integrity of the signal of interest.
Additionally, the document provides insights into the practical implementation of these filters, including the necessary computational techniques and algorithms. It highlights the significance of single-sided bandwidth and the time span for data processing, which are critical for ensuring that the filters operate effectively within the constraints of the data being analyzed.
The work was conducted at the Jet Propulsion Laboratory (JPL) under the auspices of the National Aeronautics and Space Administration (NASA), and it does not endorse any specific commercial products or services. The document serves as a comprehensive guide for engineers and scientists involved in signal processing, offering methodologies that can be applied to various datasets encountered in space exploration and Earth observation.
In summary, this document is a valuable resource for understanding FIR filter design and its application in processing time series data, particularly in the context of NASA's scientific missions. It combines theoretical principles with practical guidance, making it a useful reference for professionals in the field of digital signal processing.
