A recently developed routing algorithm for broadcasting in an ad hoc wireless communication network takes account of, and exploits, the spatial relationships among the locations of nodes, in addition to transmission power levels and distances between the nodes. In contrast, most prior algorithms for discovering routes through ad hoc networks rely heavily on transmission power levels and utilize limited graph-topology techniques that do not involve consideration of the aforesaid spatial relationships. The present algorithm extracts the relevant spatial-relationship information by use of a construct denoted the relative-neighborhood graph (RNG).
The RNG algorithm is best described by reference to, and comparison with, two prior algorithms: one based on a construct denoted the minimum-radius (minR) graph, the other based on a construct denoted the minimum spanning tree (MST). The minR algorithm starts from the assumption that every node must use the same transmission radius, d. [As used here, "transmission radius" does not signify radius as the term is commonly understood; instead, it signifies an effective radius that depends on the ratio between the transmission power and the bit rate.] An iterative binary search is performed to find the smallest d that guarantees connectivity of the network. On each iteration, a graph with transmission radius d is computed. If the graph is found to be connected, then d is decreased for the next iteration. The algorithm stops at the finding of the value of d such that the graph is connected but at the next smaller increment of d, the graph is partitioned into two or more sub-graphs. The number of operations needed to compute the minR graph is proportional to a number of the order of n2log(s), where n is the number of nodes and s is the length of the side of a square of the same area as that containing the nodes.
The RNG of a set of nodes is the graph constructed according to the rule that any two of the nodes separated by distance l are connected by an edge only if there does not exist another node at a distance <l from either first-mentioned node. The two nodes so connected are denoted relative neighbors. In the RNG, unlike in the minR graph, a different radius can be used for each pair of nodes. The RNG is a super-graph of the MST (which is described next) and a sub-graph of the graph of the Delaunay triangulation, which is a technique for connecting pairs of grid points with straight lines in such a way as to obtain an optimum tessellation of a grid area. The number of operations needed to compute the RNG is proportional to a number of the order of nlog(n).
The MST is a sub-graph of the RNG. Therefore, one can use the RNG in the computation of the MST. An edge is included in the MST if it does not create a cycle in the graph. The construction of the MST involves disjoint sets. Nodes that are connected are placed in the same set. If a tested edge connects two nodes belonging to different sets, then the edge is added to MST and the two sets are united. If a tested edge connects two nodes belonging to the same set, then this edge creates a cycle and it is rejected. The number of operations needed to compute the MST is bounded by a number proportional to n, given that the RNG was pre-computed.
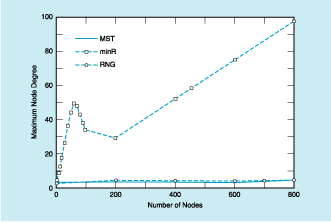
The comparison among the three algorithms is unavoidably complex because each offers both advantages and disadvantages with respect to the others. The figure presents an example of comparison with respect to the maximum node degree, which is only one of several different measures applied to results of computational simulations. The only general conclusion that one can draw from the comparisons by this and other measures is that the graph properties of the RNG are good, relative to those of the minR graph and the MST and that the RNG is suitable for efficient dissemination of information to all the nodes of a network.
This work was done by Clayton Okino and Esther Jennings of Caltech for NASA's Jet Propulsion Laboratory. For further information, access the Technical Support Package (TSP) free on-line at www.techbriefs.com/tsp under the Electronics/Computers category.
This algorithm is available for commercial licensing. Please contact Don Hart of the California Institute of Technology at (818) 393-3425. Refer to NPO-30453.
This Brief includes a Technical Support Package (TSP).

Routing Algorithm Exploits Spatial Relations
(reference NPO-30453) is currently available for download from the TSP library.
Don't have an account?
Overview
The document is a technical support package prepared under the sponsorship of NASA, detailing a Spatial Dependent Route Discovery Algorithm developed by Esther H. Jennings and Clayton M. Okino at the Jet Propulsion Laboratory (JPL). The focus of the research is on improving information dissemination in ad-hoc wireless networks, particularly through the use of innovative graph topologies.
The paper begins by addressing the challenges of successful information broadcasting in networks where nodes are uniformly distributed without prior knowledge of the network topology. It highlights that traditional algorithms often rely heavily on transmission power and limited graph techniques, which do not adequately consider the spatial relationships between nodes. This limitation can lead to inefficient routing and increased energy consumption.
To tackle these issues, the authors propose the use of a relative neighborhood graph (RNG) as a means to extract inherent patterns based on the spatial arrangement of nodes. This approach aims to create a "natural" power-aware route topology that enhances connectivity and reduces the number of transmissions required for successful information dissemination.
The document outlines three classes of topologies that were analyzed through simulations: minimum radius graphs, relative neighborhood graphs, and minimum spanning trees. Each topology was evaluated based on key graph properties such as radius, hop diameter, edge density, and node degree, which influence the efficiency of communication and the overall performance of the network.
The findings indicate that the relative neighborhood graph possesses favorable properties for efficient information dissemination, making it a suitable choice for ad-hoc networks. The authors emphasize the importance of connectivity among nodes, as it directly impacts the effectiveness of information sharing, particularly in scenarios where nodes may be sparsely distributed.
In conclusion, the research presents a novel approach to route discovery in ad-hoc networks by refining methods for establishing power-aware topologies. By utilizing the relative neighborhood graph, the authors aim to minimize the set of legitimate route paths while maintaining essential graph properties, potentially leading to reduced route tables and improved network performance. This work contributes to the ongoing development of cooperative sensor networks and enhances the efficiency of communication in dynamic environments.

