A rectangular-constellation-based blind-equalization (RECBEQ) technique implemented by a real-time, recursive algorithm has been developed to improve the performances of radio receivers in recovering unknown signals that are modulated with digital information and that have been distorted in propagation by multipath channels and carrier offsets. The technique is so named because it is intended specifically to enable the equalization of large-order rectangular signal constellations; for example, that of quadrature amplitude modulation (QAM).

Blind equalization provides for the recovery of unknown signals via a finite-dimensional linear projection of a channel output data vector; namely,
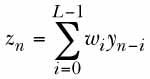
where zn is the complex output sample from the blind equalizer at the nth sampling interval, wi is the ith of L blind-equalizer coefficients, and yj is the jth complex sample from the unknown channel. The latter sample can be expressed as a convolution of the sampled channel impulse response fkwith an unknown sequence of independent and identically distributed source symbolsal; that is,
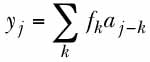
This equalization process is said to be "blind" because the wis are derived from available channel output data only, without knowledge of either the transmitted signal waveform or the linear channel.
The present blind-equalization technique belongs to a class of such techniques in which the wis are chosen to maximize or minimize objective functions (e.g., cost functions). The objective function for this technique is derived from a uniformly most powerful (UMP) scale-invariant hypothesis test between factored (rectangular) generalized Gaussian distributions. The net result of the derivation is the following time-recursive equation for updating the blind-equalizer coefficients:
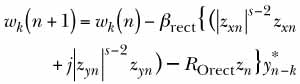
where βrect is a positive "step size" which controls the rate of adaptation (smaller values of βrect result in lower adaptation rates); the subscripts x and y denote the real and imaginary parts, respectively, of the affected quantities; s is a positive constant, greater than 2, which helps determine the steady-state performance of the equalizer (larger values of s yield lower steady-state adaptation noise but result in greater implementation complexity and greater sensitivity to additive receiver noise - it has been observed that s = 8 provides a good tradeoff between algorithm adaptation noise in steady state and sensitivity to additive receiver noise); ROrect is a positive constant which controls the scale of the equalized constellation at convergence and is given by:
![]()
and E( )is the expectation operator. The equation for wk(n+ 1) converges rapidly for input rectangular constellations distorted by multipath.
When residual carrier offsets are present, the receiver must also include a data-directed phase-locked loop (PLL). Part of the figure depicts a conventional receiver architecture that incorporates a data PLL along with an older blind equalizer of a type called "CMA" (constant-modulus algorithm). The equalizer output is phase-corrected ("derotated") by the PLL output, which is driven by symbol decisions based on the phase-corrected equalizer output. This architecture is viable because the CMA is not affected by phase rotations of the input signal constellation, and therefore phase correction can occur downstream from the CMA equalizer.
Unlike the CMA, the RECBEQ algorithm is sensitive to the phase orientation. Extensive tests have revealed that the RECBEQ algorithm can acquire a rotating rectangular constellation, but not at the same level of precision that would be achieved if the constellation were static. This finding led to the development of the modified architecture, also shown in the figure. Here, the input to the RECBEQ equalizer is phase-corrected by the PLL output, which again, is driven by symbol decisions based directly on the equalizer output. In this architecture, the RECBEQ initially equalizes the rotating constellation to such an extent that the PLL can lock up and finalize the joint equalization/carrier-recovery process.
Results of computational tests show that for rectangular constellations, the RECBEQ algorithm converges much more quickly, to lower-noise solutions, than does the CMA. For other, more-rounded constellations [e.g., those of M-ary-phase-shift keying (MPSK)], the CMA performs better. Computationally, both algorithms are comparable.
This work was done by Edgar Satorius of Caltech and James Mulligan of TASC for NASA's Jet Propulsion Laboratory. NPO-20324
This Brief includes a Technical Support Package (TSP).

Algorithm for equalizing rectangular signal constelations
(reference NPO20324) is currently available for download from the TSP library.
Don't have an account?
Overview
The document presents a technical support package detailing a novel algorithm for equalizing large-order rectangular signal constellations, specifically focusing on quadrature amplitude modulation (QAM). Developed by inventors James J. Mulligan and Edgar H. Satorius at NASA's Jet Propulsion Laboratory, this technique addresses the challenges posed by multipath channels and carrier offsets that can distort transmitted signals.
The primary motivation behind this work is to create a real-time, time-recursive blind equalization algorithm that converges rapidly to effectively equalize signals distorted during transmission. Traditional equalization methods, such as the constant modulus algorithm, often struggle with large-order rectangular constellations, leading to slower convergence and less effective signal recovery. The proposed algorithm significantly improves performance by leveraging a cost function tailored for these specific signal constellations.
The document outlines the novelty of the invention, emphasizing its ability to achieve quicker convergence to a cleaner solution compared to conventional methods. By extending the concept of uniformly most powerful, scale-invariant tests into the complex domain, the researchers designed an equalizer that is particularly effective for large-order rectangular constellations. This advancement is crucial for applications in data communication systems where signal integrity is paramount.
The technical disclosure section elaborates on the problem that led to the development of this algorithm, highlighting the need for efficient equalization techniques in real-time applications. The solution provided by the RECBEQ technique not only enhances the recovery of distorted signals but also opens avenues for improved performance in various communication systems.
Additionally, the document includes a disclaimer regarding the endorsement of any specific commercial products or processes mentioned, clarifying that the work was conducted under a contract with NASA. The technical support package serves as a comprehensive overview of the algorithm's development, its advantages over prior art, and its potential applications in enhancing data communication reliability.
In summary, this document encapsulates a significant advancement in signal processing technology, offering a robust solution for equalizing rectangular signal constellations and improving the performance of communication systems in the face of distortion challenges.

