Better Modeling of Electrostatic Discharge in an Insulator

NASA’s Jet Propulsion Laboratory, Pasadena, California

An improved mathematical model has been developed of the time dependence of buildup or decay of electric charge in a high-resistivity (nominally insulating) material. The model is intended primarily for use in extracting the DC electrical resistivity of such a material from voltage-vs.- current measurements performed repeatedly on a sample of the material over a time comparable to the longest characteristic times (typically of the order of months) that govern the evolution of relevant properties of the material. This model is an alternative to a prior simplistic macroscopic model that yields results differing from the results of the time-dependent measurements by two to three orders of magnitude.

The present model is based on the Kohlrausch relaxation law, named after its author, who first reported a long-lasting dielectric relaxation in 1854. Since then, the Kohlrausch law has been used to describe a myriad of physical phenomena. Kohlrausch relaxation is also known as stretched exponential relaxation because the time-dependent value of a Kohlrausch-relaxing quantity of interest is proportional to the stretched exponential function exp[(–t/τ)^β] where t is time, τ is a characteristic relaxation time of the material in question, and β is a parameter (sometimes denoted the Kohlrausch exponent) that has a value between 0 and 1. Many microscopic models of transport in distributed sys-tems (e.g., electron hopping, dipole fluctuation) have shown to result in Kohlrausch dependences of macroscopic observables.

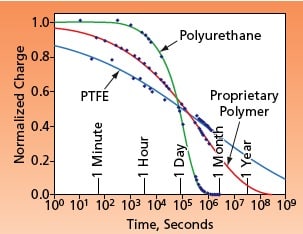
In general, whichever model is used, the DC electrical resistivity of a material sample subjected to long-term charge-decay measurements is calculated from parameters used to fit the model to the measurement data. Various methods that have been used to fit simplistic macroscopic models to measurement data involve large numbers of fitting parameters and involve user-dependent fitting calculations. In contrast, the Kohlrausch-relaxationbased model involves the minimum possible number of fitting parameters, and the associated fitting calculations are not user-dependent.

The applicability of the present model and its superiority to the prior macroscopic model have been demonstrated through the closeness with which this model has been shown to fit experimental data on normalized charge over 5 to 6 orders of magnitude in time (for example, see figure). Although the validity of DC-resistivity values derived from fitting parameters of this model has yet to be demonstrated, the mere fact that these resistivity values differ from those obtained by application of the prior macroscopic model to the same experimental data indicates the need for further research to answer the questions of what are the relevant properties of the affected materials and what are the proper methods of determining these properties.

This work was done by Mihail Petkov of Caltech for NASA’s Jet Propulsion Laboratory. For more information, contact This email address is being protected from spambots. You need JavaScript enabled to view it.. NPO-44868

---

---