A method is proposed for end-toend, full aperture testing of large-aperture telescopes using an innovative variation of a Hartmann mask. This technique is practical for telescopes with primary mirrors tens of meters in diameter and of any design. Furthermore, it is applicable to the entire optical band (near IR, visible, ultraviolet), relatively insensitive to environmental perturbations, and is suitable for ambient laboratory as well as thermal-vacuum environments. The only restriction is that the telescope optical axis must be parallel to the local gravity vector during testing.
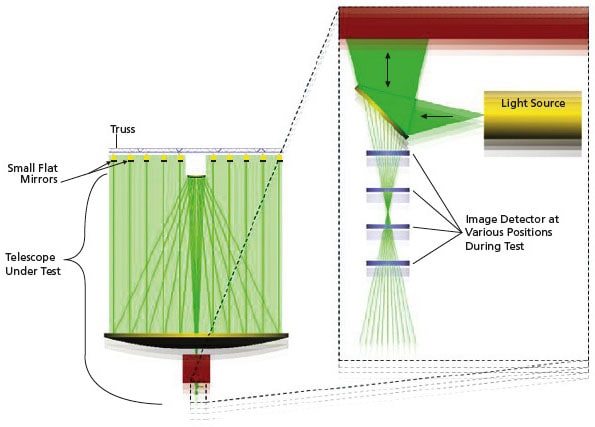
The standard Hartmann test utilizes an array of pencil beams that are cut out of a well-corrected wavefront using a mask. The pencil beam array is expanded to fill the full aperture of the telescope. The detector plane of the telescope is translated back and forth along the optical axis in the vicinity of the nominal focal plane, and the centroid of each pencil beam image is recorded. Standard analytical techniques are then used to reconstruct the telescope wavefront from the centroid data. The expansion of the array of pencil beams is usually accomplished by double passing the beams through the telescope under test. However, this requires a well-corrected, autocollimation flat, the diameter or which is approximately equal to that of the telescope aperture. Thus, the standard Hartmann method does not scale well because of the difficulty and expense of building and mounting a well-corrected, large aperture flat.
The innovation in the testing method proposed here is to replace the large aperture, well-corrected, monolithic autocollimation flat with an array of small-aperture mirrors. In addition to eliminating the need for a large optic, the surface figure requirement for the small mirrors is relaxed compared to that required of the large autocollimation flat. The key point that allows this method to work is that the small mirrors need to operate as a monolithic flat only with regard to tip/tilt and not piston because in collimated space piston has no effect on the image centroids. The problem of aligning the small mirrors in tip/tilt requires a two-part solution. First, each mirror is suspended from a two-axis gimbal. The orientation of the gimbal is maintained by gravity. Second, the mirror is aligned such that the mirror normal is parallel to gravity vector. This is accomplished interferometrically in a test fixture. Of course, the test fixture itself needs to be calibrated with respect to gravity.
Another significant advantage of the array of gimbaled small mirrors is the tolerance of the apparatus to thermal and mechanical perturbations. The individual mirrors are not affected by thermal distortions of the array structure because their orientation is self-correcting. That is, the pointing is maintained by gravity, not their supporting structure. Likewise, vibrations will cause the mirrors to sway about their equilibrium position. Thus, integrating the pencil beam image centroids over a sufficiently long period of time will make the measurements insensitive to vibration.
This work was done by Robert P. Korechoff and Jeffrey M. Oseas of Caltech for NASA’s Jet Propulsion Laboratory. For more information, download the Technical Support Package (free white paper) at www.techbriefs.com/tsp under the Physical Sciences category. NPO-46118
This Brief includes a Technical Support Package (TSP).

Self-Referencing Hartmann Test for Large-Aperture Telescopes
(reference NPO-46118) is currently available for download from the TSP library.
Don't have an account?
Overview
The document titled "Self-Referencing Hartmann Test for Large-Aperture Telescopes" is a technical support package developed by NASA's Jet Propulsion Laboratory. It outlines a novel testing technique designed to evaluate large aperture telescopes in a practical manner, addressing the challenges associated with traditional Hartmann testing methods.
Traditional Hartmann testing involves measuring the performance of a device under test (DUT) using a collimated light source. However, for large aperture systems, creating a well-corrected light source becomes impractical, leading to significant uncertainties in performance assessment. The self-referencing Hartmann test aims to overcome these limitations by utilizing a different approach that allows for more accurate evaluations of large telescopes.
Key issues addressed in the document include the alignment of mounting surfaces, the potential distortion of the support structure due to temperature changes or vibrations, and the effects of gravity on mirror alignment. The proposed solution involves the use of gimbaled interfaces for mirror installation, which allows mirrors to maintain alignment with respect to gravity, regardless of fabrication tolerances or structural distortions. This gimbaled mirror assembly technique enhances the stability and accuracy of the telescope's performance.
The document also discusses the implementation of an array of shutters in front of each mirror to aid in identifying individual pencil beam coordinates. This setup allows for controlled opening and closing of shutters to facilitate spot identification without interfering with the gimbals' free movement. Additionally, the entire gimbaled mirror array can be translated to achieve more comprehensive coverage of the aperture, although this introduces its own set of challenges.
Furthermore, the document highlights the impact of gravity on large aperture telescopes, noting that even slight variations in the gravity vector can affect mirror alignment. It suggests that these effects can be accounted for through careful tracking during assembly or through analytic correction methods.
Overall, the self-referencing Hartmann test represents a significant advancement in the testing of large aperture telescopes, providing a more reliable and efficient means of assessing their performance. The document serves as a valuable resource for researchers and engineers involved in aerospace technology, offering insights into innovative testing methodologies and their practical applications.

