Integrated circuits of a proposed type based on quantum-dot cellular automata (QCA) would implement permutation matrices. These circuits would serve as prototype building blocks for demonstrating the feasibility of quantum-dot-based computing and for the further development of increasingly complex and increasingly capable quantum-dot-based computing circuits. Permutation matrices were chosen as part of the basis of this development because (1) they play a major role in fast transforms (e.g., the fast Fourier, cosine, and Hartley transforms) that arise in the processing of signals and images and that are amenable to parallel computing by application-specific integrated circuits and (2) in principle, they could be implemented directly in the patterns of circuits of the proposed type.

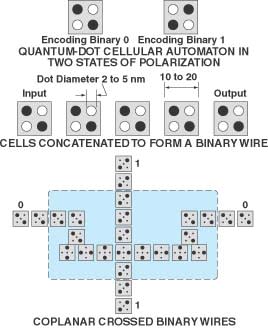
Figure 1. Quantum-Dot Cellular Automata can be assembled into binary wires, which can cross without adverse effects.
As the development of very-large-scale integrated (VLSI) circuitry approaches the lower limits of practical feature sizes, QCA may offer an alternative that will enable further miniaturization. Of equal if not greater significance is the expectation that QCA may enable a great simplification of VLSI circuit patterns while affording capabilities that, heretofore, have not existed:

At present, wherever two wires in a VLSI circuit cross each other, the wires must not be in the same plane; that is, there must be a layer of electrical insulation between them (unless, of course, they are meant to be connected at the intersection). Much of the complexity and hence cost of VLSI design is associated with minimization of data routing and assignment of layers to minimize crossing of wires. The proposed circuits would enable one to take advantage of a unique feature of QCA; namely, the possibility of coplanar crossing of signal paths. This feature is what makes it possible, in principle, to implement various permutation matrices directly in coplanar patterns of quantum-dot circuit elements. Such a direct and compact implementation would be extremely costly if not impossible in conventional complementary metal oxide/semiconductor (CMOS) VLSI integrated circuitry.

Figure 2. A Simple QCA Circuit would implement the downshift permutation matrix Q4
A quantum-dot cellular automaton contains four quantum dots positioned at the corners of a square (see Figure 1). The cell contains two extra mobile electrons that can tunnel (in the quantum-mechanical sense) between neighboring dots. Tunneling out of the cell is assumed to be completely suppressed by the potential barriers between neighboring cells. The Coulomb repulsion between the two electrons tends to make them occupy antipodal dots in the cell. For an isolated cell, there are two energetically equivalent arrangements (denoted polarization states) of the extra electrons. The cell polarization is used to encode binary information.

The polarization of a nonisolated cell depends on interactions with neighboring cells. The interaction between cells is one of Coulomb repulsion only (no current flows between cells) and provides the basis for computing with QCA. Theoretically, universal logic gates and binary wires could be constructed by assembling QCA of suitable design in suitable patterns. As to the possibility of coplanar crossing of signal paths without adverse effect, a compete theoretical explanation would exceed the space available for this article, but one can gain a partial, qualitative understanding from the illustration of crossed binary QCA wires in the bottom part of Figure 1.

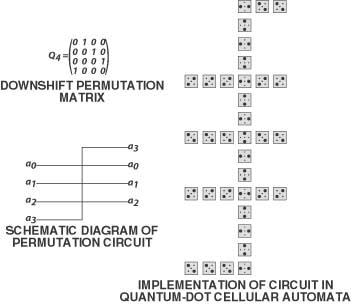
One of the fundamental permutation matrices is the downshift permutation matrix, which is given by

where n is the number of elements to be permuted. Figure 2 illustrates a proposed QCA circuit that would implement the permutation matrix Q4.

This work was done by Amir Fijany, Nikzad Toomarian, and Matthew Spotnitz of Caltech for NASA's Jet Propulsion Laboratory. For further information, access the Technical Support Package (TSP) free on-line at www.nasatech.com/tsp  under the Electronics & Computers category.

NPO-20801

Topics:
Assembling Automation Electronic equipment Electronics & Computers Insulation Integrated circuits Manufacturing processes Robotics
This Brief includes a Technical Support Package (TSP).
Document cover
Implementing Permutation Matrices by Use of Quantum Dots

(reference NPO-20801) is currently available for download from the TSP library.

Don't have an account?

Magazine cover
NASA Tech Briefs Magazine

This article first appeared in the October, 2001 issue of NASA Tech Briefs Magazine (Vol. 25 No. 10).

Read more articles from the archives here.

Overview

The document discusses the innovative application of quantum-dot cellular automata (QCA) in the design and implementation of permutation matrices, a crucial component in various computational tasks. The research is conducted by a team from the Jet Propulsion Laboratory (JPL) at the California Institute of Technology, under the auspices of NASA.

Quantum-dot cellular automata represent a paradigm shift in computing technology, moving away from traditional transistor-based designs. QCA utilizes the quantum properties of electrons in nanoscale structures to perform computations, allowing for the creation of circuits that are smaller, faster, and more energy-efficient than their conventional counterparts. This technology is particularly relevant as the limitations of current integrated circuits become more pronounced, necessitating the exploration of alternative computing methods.

The document outlines the theoretical framework and practical implications of using QCA for implementing permutation matrices. Permutation matrices are essential in various applications, including cryptography, signal processing, and data organization. The ability to efficiently implement these matrices using QCA could lead to significant advancements in computational speed and efficiency.

The authors detail the methodology employed in their research, including the design of QCA circuits that can perform the necessary operations for permutation matrices. They also discuss the potential benefits of this approach, such as reduced circuit complexity and improved performance metrics compared to traditional methods.

Furthermore, the document emphasizes the importance of this research in the broader context of quantum computing and its potential to revolutionize the field. By leveraging the unique properties of quantum mechanics, QCA could pave the way for new types of computing architectures that are capable of handling increasingly complex tasks.

In conclusion, the document presents a compelling case for the adoption of quantum-dot cellular automata in the implementation of permutation matrices, highlighting its potential to transform computing as we know it. The research conducted at JPL not only contributes to the academic understanding of QCA but also has practical implications for the future of technology, positioning it as a key player in the evolution of computational systems.