A mathematical model constructed within a theoretical framework applicable to direct numerical simulation (DNS) predicts the behavior of evaporating liquid drops entrained in a turbulent shear layer.
In the model, liquid drops are assumed to be dispersed at low volume fraction (though not necessarily low mass fraction) in a carrier gas. All chemical species are assumed to be calorically perfect. Gravitation is neglected. It is assumed that values of the viscosity, thermal conductivity, and species diffusivity of the gas phase can be prescribed, independently of the local mixture fraction.
The compressible conservation equations for mass, momentum, and energy for the gas phase are formulated in an Eulerian reference frame and include terms to account for exchanges of mass, momentum, and energy with the drops. The drops are assumed spherical and their internal temperature is assumed uniform.
Each drop is tracked in a time-accurate manner in a Lagrangian reference frame; these equations include terms for the drag exerted on each drop by the surrounding flowing gas. Each drop is assumed to exchange heat with the gas phase through convection and conduction only, since this study is performed at low temperature. Evaporation is represented by the nonequilibrium Langmuir-Knudsen law. The model accounts for complete two-way phase coupling (both gas-to-liquid and liquid-to-gas) of mass, momentum, and energy based on a thermodynamically self-consistent specification of vapor enthalpy, internal energy, and latent heat of vaporization.
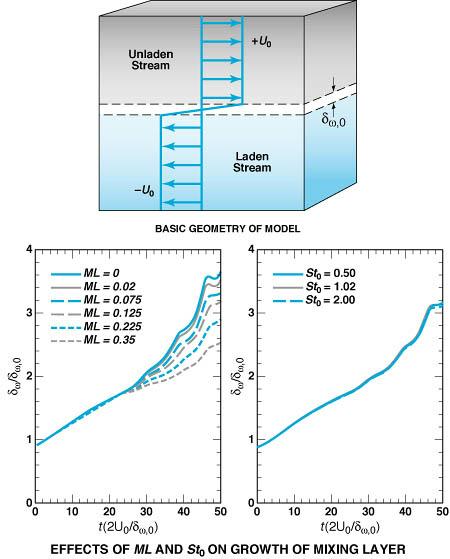
The model has been used to simulate the behavior of a three-dimensional, temporally developing, initially isothermal gas mixing layer formed by the merging of an airstream with a gas stream laden with hydrocarbon drops. Effects of the initial liquid-mass-loading ratio (ML), the initial Stokes number (St0), the initial temperature of the drops, and the three-dimensionality of the flow on the evolution of the mixing layer were examined. The dominant parameter affecting the flow was found to be ML (for example, see figure). The laden stream was found to become saturated before evaporation was complete, at all but the smallest values of ML. Drops in the mixing layer were observed to be centrifuged out of regions of high vorticity and to migrate toward regions of high strain in the flow, with resultant formation of concentration streaks in spanwise braid regions wrapped around peripheries of secondary streamwise vortices. Persistent regions of positive and negative slip velocity and slip temperature were identified. Other characteristics examined included variances of liquid- and gas-phase velocities and relationships among gas-velocity, drop-number-density, and thermodynamic profiles. From considerations of first and second order statistics, a comprehensive picture of the mixing layer is described.
This work was done by Josette Bellan and Richard S. Miller of Caltech for NASA's Jet Propulsion Laboratory. NPO-20434
This Brief includes a Technical Support Package (TSP).

Mathematical modeling of two-phase flow with evaporation
(reference NPO20434) is currently available for download from the TSP library.
Don't have an account?
Overview
The document is a technical support package from NASA detailing the mathematical modeling of two-phase flow with evaporation, specifically focusing on the behavior of evaporating liquid droplets within turbulent shear layers. Authored by Josette Bellan and Richard S. Miller, the report outlines the theoretical frameworks and numerical simulations used to predict the interactions between liquid droplets and gas phases in various flow conditions.
Key aspects of the study include the examination of droplet evaporation mechanisms, which are influenced by slip variables such as vapor fraction and temperature. The document discusses how these variables affect the evaporation rate and the conditions necessary to achieve saturation in the flow, thereby halting liquid evaporation. The authors introduce averaging operators to analyze the statistical properties of the droplet field, distinguishing between Eulerian (gas phase) and Lagrangian (droplet) variables.
The report also presents a detailed analysis of droplet organization and preferential concentration within the mixing layer. It highlights the importance of understanding the instantaneous structure of the dispersed droplet field, which aids in interpreting statistical results and developing turbulence models. The document includes visualizations and quantitative results that illustrate the local distribution and behavior of droplets relative to large-scale flow structures.
Furthermore, the study provides insights into the number density distribution of droplets, showcasing how contours of droplet concentration can reveal significant variations in local density compared to the initial mean density in the laden stream. The findings indicate that maximum local droplet densities can reach levels significantly higher than the initial conditions, emphasizing the dynamic nature of the flow.
Overall, this technical report serves as a foundational resource for researchers and engineers interested in the complexities of two-phase flow dynamics, particularly in applications involving evaporation processes. It underscores the significance of mathematical modeling in predicting flow behavior and informs future developments in turbulence modeling and evaporating droplet dynamics. The document is a valuable contribution to the field, providing both theoretical insights and practical implications for the study of two-phase flows.

