An improved formulation of equations of flow of a general gas mixture includes consistent boundary conditions that are applicable to real gases. An analysis of prior formulations, with focus on boundary conditions, led to the conclusion that boundary conditions based on ideal mixtures and/or perfect gases can lead to errors in computed flows of real gases. The improved formulation makes it possible to achieve greater accuracy in computation of flows of real (including chemically reactive) gas mixtures, and is expected to be especially beneficial in computing flows of supercritical fluids like those in diesel engines, gas turbine engines, rocket engines, supercritical-fluid extraction processes, and crude oil under high pressure.
The conservation equations are for general viscous fluids; however, the boundary conditions are calculated from equations of inviscid flow (Euler equations) augmented by species and energy equations. Characteristic boundary conditions are derived from a wave decomposition of the Euler equations, and wave-amplitude variations are determined from the prescribed boundary conditions on the flow variables in conjunction with a general equation of state for a real gas.
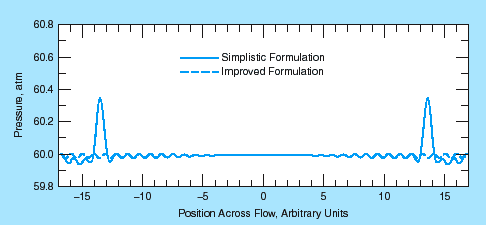
The improved formulation was tested in computations of the one-dimensional propagation of acoustic waves in a flowing supercritical mixture of nitrogen and heptane in a two-dimensional domain with nonreflecting boundaries. The results obtained with this formulation were compared with those from another formulation in which real-gas thermodynamic properties were simplistically substituted into characteristic equations derived previously for a perfect gas. The waves computed in the improved formulation were found to leave the computational domain with minimal reflection at a subsonic outflow boundary, whereas the waves computed in the simplistic formulation exhibited significant reflections at the boundaries (see figure).
Although the superiority of the improved formulation has been shown by this test, caution is in order because the characteristic-wave analysis inherently incorporates the assumption that elliptic terms act only as corrections to an essentially hyperbolic operator. Thus, diffusional terms are not parts of the consistent- boundary-condition analysis, but are used in the governing equations once a solution is sought. The condition of weak ellipticity may not always be satisfied when thermal-diffusion effects are large enough to augment the effective thermal conductivity to the point of making heat diffusion processes comparable in magnitude to convective processes.
This work was done by Josette Bellan, Nora Okong'o, and Kenneth Harstad of Caltech for NASA's Jet Propulsion Laboratory. For further information, access the Technical Support Package (TSP) free on-line at www.nasatech.com/tsp under the Physical Sciences category.
NPO-20970
This Brief includes a Technical Support Package (TSP).

Boundary Conditions for Computing Flows of Real Gas Mixtures
(reference NPO-20970) is currently available for download from the TSP library.
Don't have an account?
Overview
The document discusses advancements in boundary conditions for computing flows of real gas mixtures, particularly focusing on multicomponent perfect gas mixtures and their extension to real gases. The work, conducted by Josette Bellan, Kenneth G. Harstad, and Nora Okong at NASA's Jet Propulsion Laboratory, emphasizes the importance of accurate boundary conditions in computational fluid dynamics, especially for real gases that exhibit complex behaviors compared to ideal gases.
The improved formulation is based on the conservation equations of mass, chemical species, energy, and momentum, which are augmented by species- and energy-conservation equations and a general equation of state for real gases. This formulation incorporates additional terms, specifically the Soret and Dufour effects, which account for thermal contributions to species diffusion and heat transport due to concentration gradients, respectively. These enhancements are crucial for accurately modeling flows in applications involving supercritical fluids, such as in diesel engines, gas turbines, and rocket engines.
The document highlights the derivation of characteristic boundary conditions from the wave decomposition of the inviscid Euler equations. This approach allows for the determination of wave amplitude variations based on prescribed boundary conditions, leading to more reliable computational results. The improved formulation was tested through simulations of one-dimensional acoustic wave propagation in a supercritical nitrogen-heptane mixture, demonstrating its superiority over previous formulations that relied on simplified assumptions about real gas properties.
Results indicated that the improved formulation significantly reduced wave reflections at boundaries, which is a common issue in computational models. In contrast, the simplistic formulation led to substantial spurious reflections, highlighting the importance of using consistent boundary conditions for accurate flow predictions.
The document also cautions that while the characteristic-wave analysis provides a robust framework, it assumes that elliptic terms act merely as corrections to a hyperbolic operator. This assumption may not hold in scenarios where thermal-diffusion effects are pronounced, potentially complicating the analysis.
Overall, the work represents a significant step forward in computational fluid dynamics, offering a more accurate and reliable method for simulating the behavior of real gas mixtures, which is essential for various engineering applications in aerospace and beyond.

