According to a proposal, membranes to be used in inflatable focusing mirrors (see Figure 1) would be designed and fabricated with parabolic radial variations of thickness. More specifically, for a mirror membrane with a diameter D, the thickness (t) at a given radial distance (r) from the optical axis would be given by
t = t0(1 + Au2),
where t0 is the thickness at the center, A is a parameter described below, and u ≡ 2r/D. The reason for this proposal is that by suitable choice of A, one could ensure that upon inflation, the membrane would assume a shape that closely approximates a paraboloid — the shape required for focusing in many applications.

Past investigations of membrane mirrors have led to the conclusion that they are not suitable for imaging in visible light because their shapes when inflated differ too much from paraboloids. In particular, upon inflation, a previously flat membrane of uniform thickness assumes an oblate spheroidal shape described by a function named the "Hencky curve" after its discoverer. Although there have been suggestions that radial variations in thickness might result in inflated shapes that equal or closely approximate paraboloids, the necessary variation in thickness has not been published until now.
The proposal is justified by a mathematical derivation that starts with the classical equation for the axial deflection [z(u)] of an initially flat, elastic, thin plate (that is, membrane) of thickness t(u) that is subjected to a differential pressure and restrained by a ring as described above. The problem is to find t(u) such that z(u) would approximate the desired paraboloidal form to the desired degree of precision. The solution involves a numerical integration that leads to the conclusion that a parabolic radial variation of thickness with A = 0.42 would yield the desired inflated shape, regardless of the values of inflation pressure, deflection at the center, and focal ratio of the inflated membrane mirror.
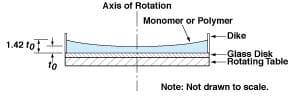
A membrane according to the proposal could be fabricated most conveniently by either of two techniques. One way would be to cast or otherwise form a membrane polymer on a convex spherical mold with a large radius of curvature that yields an acceptably close approximation to the desired shape. The other way would be to adapt a technique that has been used before to make astronomical mirrors: This technique is based on the fact that the height of a liquid on a horizontal, flat, steadily rotating table varies parabolically with radius from the axis of rotation. The table would be covered with a flat disk of glass or other smooth material, a dike to contain liquid would be placed around the periphery of the disk, the required amount of mono-meric liquid would be poured onto the disk, and the disk would be set into rotation at the speed necessary to make the thickness of the liquid at the planned outer diameter of the membrane equal to 1.42 times the thickness at the axis of rotation (see Figure 2). The mon-omer would be polymerized as the table continued to rotate, thereby locking in the parabolic radial variation with thickness.
This work was done by Aden Meinel and Marjorie Meinel of Caltech for NASA's Jet Propulsion Laboratory. For further information, access the Technical Support Package (TSP) free on-line at www.nasatech.com/tsp under the Mechanics category.
NPO-20952
This Brief includes a Technical Support Package (TSP).

Paralobic Membrane-Thickness Variation for Inflatable Mirror
(reference NPO-20952) is currently available for download from the TSP library.
Don't have an account?
Overview
The document discusses innovative approaches to the design and fabrication of inflatable mirrors, specifically focusing on the use of membranes with parabolic radial variations in thickness. Traditional inflatable mirrors, made from uniformly thick membranes, tend to deform into an aspheric shape known as the Henyey curve, which is unsuitable for high-resolution optical systems. This limitation has prompted researchers to explore alternative designs that can achieve a more desirable parabolic shape.
The key innovation presented is the introduction of a quadratic radial variation in membrane thickness. Computational modeling has shown that this specific variation can closely approximate a parabolic surface when the mirror is inflated. The document outlines the motivation behind this research, emphasizing the need for improved optical performance in inflatable mirrors used in space telescopes and other applications.
The proposed solution involves either casting or forming membranes with a parabolic thickness variation. This can be achieved by using a polished substrate with a long convex radius of curvature or by casting the membrane on a pre-formed parabolic shape on a slowly rotating table. This method allows for the creation of pre-shaped membranes that, when inflated, will result in a parabolic mirror capable of supporting high-resolution optical designs.
The document also acknowledges contributions from various associates at the Jet Propulsion Laboratory (JPL) and highlights the collaborative nature of the research. It emphasizes the importance of integrating new approaches to solve longstanding challenges in the field of optics and aerospace technology.
In summary, the document presents a significant advancement in the design of inflatable mirrors, proposing a method to achieve a parabolic shape through controlled variations in membrane thickness. This innovation has the potential to enhance the performance of optical systems in space exploration and other high-precision applications, marking a step forward in the development of ultra-lightweight space telescopes.

